Công thức tính diện tích tam giác vuông
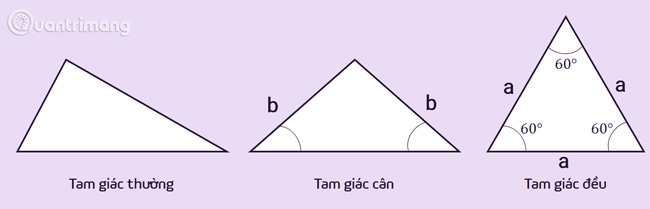
Tam giác thường: là tam giác cơ bản nhất, có độ dài các cạnh khác nhau, số đo góc trong cũng khác nhau. Tam giác thường cũng có thể bao gồm các trường hợp đặc biệt của tam giác.
Tam giác cân: là tam giác có hai cạnh bằng nhau, hai cạnh này được gọi là hai cạnh bên. Đỉnh của một tam giác cân là giao điểm của hai cạnh bên. Góc được tạo bởi đỉnh được gọi là góc ở đỉnh, hai góc còn lại gọi là góc ở đáy. Tính chất của tam giác cân là hai góc ở đáy thì bằng nhau.
Tam giác đều: là trường hợp đặc biệt của tam giác cân có cả ba cạnh bằng nhau. Tính chất của tam giác đều là có 3 góc bằng nhau và bằng 60.
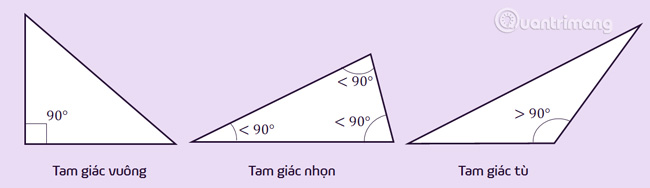
Tam giác vuông: là tam giác có một góc bằng 90 (là góc vuông).
Tam giác tù: là tam giác có một góc trong lớn hơn lớn hơn 90(một góc tù) hay có một góc ngoài bé hơn 90
(một góc nhọn).
Tam giác nhọn: là tam giác có ba góc trong đều nhỏ hơn 90 (ba góc nhọn) hay có tất cả góc ngoài lớn hơn 90
(sáu góc tù).
Tam giác vuông cân: vừa là tam giác vuông, vừa là tam giác cân.
Công thức diện tích tam giác
1. Tính diện tích tam giác thường
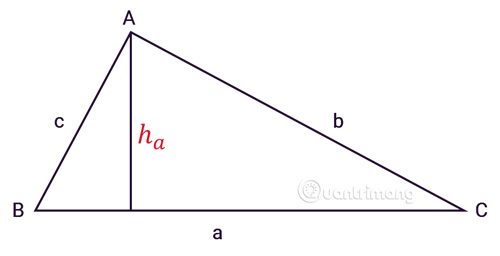
Tam giác ABC có ba cạnh a, b, c, ha là đường cao từ đỉnh A như hình vẽ:
Diện tích tam giác bằng ½ tích của chiều cao hạ từ đỉnh với độ dài cạnh đối diện của đỉnh đó.
b. Tính diện tích tam giác khi biết một góc
Diện tích tam giác bằng ½ tích hai cạnh kề với sin của góc hợp bởi hai cạnh đó trong tam giác.
c. Tính diện tích tam giác khi biết 3 cạnh bằng công thức Heron.
Sử dụng công thức Heron đã được chứng minh:
Có thể viết lại bằng công thức:
d. Tính diện tích bằng bán kính đường tròn ngoại tiếp tam giác (R).
Lưu ý: Cần phải chứng minh được R là bán kính đường tròn ngoại tiếp tam giác.
e. Tính diện tích bằng bán kính đường tròn nội tiếp tam giác (r).
2. Tính diện tích tam giác cân
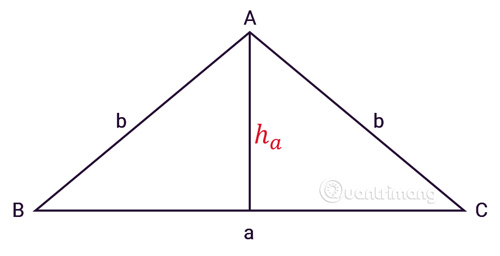
Tam giác cân ABC có ba cạnh, a là độ dài cạnh đáy, b là độ dài hai cạnh bên, ha là đường cao từ đỉnh A như hình vẽ:
Áp dụng công thức tính diện tích thường, ta có công thức tính diện tích tam giác cân:
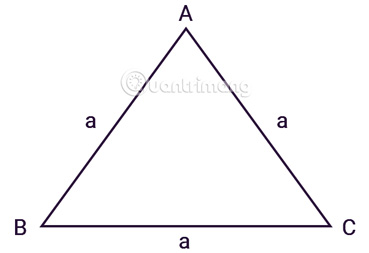
3. Tính diện tích tam giác đều
Tam giác đều ABC có ba cạnh bằng nhau, a là độ dài các cạnh như hình vẽ:
Áp dụng định lý Heron để suy ra, ta có công thức tính diện tích tam giác đều:
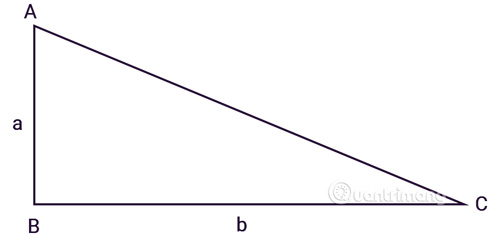
4. Tính diện tích tam giác vuông
Tam giác ABC vuông tại B, a, b là độ dài hai cạnh góc vuông:
Áp dụng công thức tính diện tích thường cho diện tích tam giác vuông với chiều cao là 1 trong 2 cạnh góc vuông và cạnh đáy là cạnh còn lại.
Công thức tính diện tích tam giác vuông:
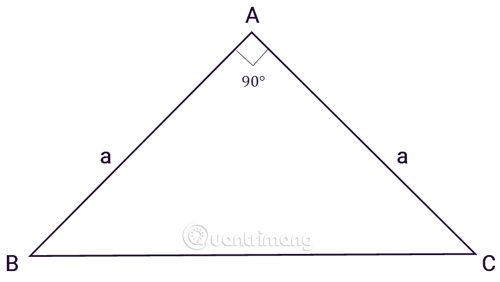
5. Tính diện tích tam giác vuông cân
Tam giác ABC vuông cân tại A, a là độ dài hai cạnh góc vuông:
Áp dụng công thức tính diện tích tam giác vuông cho diện tích tam giác vuông cân với chiều cao và cạnh đáy bằng nhau, ta có công thức:
Công thức tính chu vi hình tam giác
1. Cách tính chu vi tam giác thường
Công thức tính chu vi hình tam giác thường: Chu vi tam giác bằng độ dài tổng ba cạnh của tam giác đó
Trong đó: P là chu vi tam giác, a, b, c là 3 cạnh của hình tam giác đó
Dựa theo cách tính này, chúng ta cũng có thể tìm được cách tính nửa chu vi tam giác như sau: 1/2 P = (a+b+c)/2
Ví dụ 1: Tính chu vi tam giác lớp 2
Cho tam giác với độ dài các cạnh lần lượt là 3cm , 4 cm, 5 cm. Yêu cầu tính chu vi của tam giác đó.
Lời giải: Dựa theo công thức tính chu vi tam giác, ta có: P = a + b+ c.
Theo dữ liệu bài ra thì: a = 3 cm, b = 4 cm, c = 5cm
Như vậy, chu vi của tam giác đã cho là: P = 3 + 4 + 5 = 12 cm
Ví dụ 2: Tính chu vi tam giác khi biết 3 cạnh
Cho tam giác với độ dài 2 cạnh bên lần lượt là 3, 4 cm. Biết cạnh còn lại của tam giác có độ dài gấp 2 lần tổng tam giác còn lại. Hãy tính chu vi tam giác đó.
Gọi tam giác cần tính chu vi là ABC
Theo bài ra ta có: AB = 3cm, AC = 4 cm và BC = 2 (AB + AC)
Như vậy, chiều dài cạnh còn lại của tam giác là: BC = 2 (AB + AC) = 14 cm
Chu vi tam giác ABC lúc này sẽ bằng: P (ABC) = AB + AC + BC = 3 + 4 + 14 = 19 cm
2. Cách tính chu vi tam giác vuông
Khái niệm: Tam giác vuông là tam giác có một góc là góc vuông
– Công thức tính chu vi tam giác vuông: P= a + b + c
+ a và b : Hai cạnh của tam giác vuông
+ c là cạnh huyền của tam giác vuông.
3. Cách tính chu vi tam giác cân
Khái niệm: Tam giác cân là tam giác có 2 cạnh bên bằng nhau.
– Công thức tính chu vi tam giác cân: P = 2 a + c
Trong đó a : Hai cạnh bên của tam giác cân, c là đáy của tam giác.
Công thức tính chu vi tam giác này cũng được áp dụng để tính chu vi của tam giác vuông cân (tam giác có 1 góc vuông và 2 cạnh bên bằng nhau)
4. Cách tính chu vi tam giác đều
Khái niệm: Tam giác đều là tam giác có 3 cạnh bằng nhau
– Công thức tính chu vi tam giác đều: P = 3 x a
Trong đó: P là chu vi tam giác đều, a là chiều dài cạnh của tam giác
Công thức tính góc trong tam giác
Trong lượng giác, định lý cos biểu diễn sự liên quan giữa chiều dài của các cạnh của một tam giác phẳng với cosin của góc tương ứng:
- {\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos \gamma \,}
- {\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos C\,}
Công thức trên cũng có thể được viết dưới dạng:
- {\displaystyle \cos C={\frac {a^{2}+b^{2}-c^{2}}{2ab}}\,}
Định lý cos khái quát định lý Pytago (định lý Pytago là trường hợp riêng trong tam giác vuông): nếu γ là góc vuông thì cos γ = 0, và định lý cos trở thành định lý Pytago:
- {\displaystyle c^{2}=a^{2}+b^{2}\,}
Định lý cos được dùng để tính cạnh thứ ba khi biết hai cạnh còn lại và góc giữa hai cạnh đó, hoặc tính các góc khi chỉ biết chiều dài ba cạnh của một tam giác.
Định lý cos được biểu diễn tương tự cho hai cạnh còn lại:
- {\displaystyle a^{2}=b^{2}+c^{2}-2bc\cos \alpha \,}
- {\displaystyle b^{2}=a^{2}+c^{2}-2ac\cos \beta \,}
Hình 3 – Ứng dụng của định lý cos: tìm cạnh chưa biết và góc chưa biết.
Định lý cos được dùng trong phép đạc tam giác để giải một tam giác hoặc một đường tròn. Ví dụ trong Hình 3, định lý cos được dùng để tìm:
cạnh thứ ba của một tam giác nếu đã biết hai cạnh còn lại và góc giữa chúng:
{\displaystyle \,c={\sqrt {a^{2}+b^{2}-2ab\cos \gamma }}\,;}{\displaystyle \,c={\sqrt {a^{2}+b^{2}-2ab\cos \gamma }}\,;}
ba góc nếu biết ba cạnh của tam giác
{\displaystyle \,\gamma =\arccos \left({\frac {a^{2}+b^{2}-c^{2}}{2ab}}\right)\,;}{\displaystyle \,\gamma =\arccos \left({\frac {a^{2}+b^{2}-c^{2}}{2ab}}\right)\,;}
cạnh thứ ba nếu biết hai cạnh còn lại và góc đối diện một trong hai cạnh đó:
{\displaystyle \,a=b\cos \gamma \pm {\sqrt {c^{2}-b^{2}\sin ^{2}\gamma }}\,.}{\displaystyle \,a=b\cos \gamma \pm {\sqrt {c^{2}-b^{2}\sin ^{2}\gamma }}\,.}
Công thức thứ ba có được nhờ giải phương trình bậc hai a2 − 2ab cos γ + b2 − c2 = 0 với ẩn a. Phương trình này có hai nghiệm dương nếu b sin γ < c < b, một nghiệm dương nếu c ≥ b hoặc c = b sin γ, và vô nghiệm nếu c < b sin γ.
Chứng minh
Sử dụng công thức tính khoảng cách
Trong hệ tọa độ Descartes, cho tam giác ABC có ba cạnh a, b, c và γ là góc đối diện cạnh c với tọa độ ba đỉnh lần lượt là
{\displaystyle A=(b\cos \gamma ,\ b\sin \gamma ),\ B=(a,\ 0),\ C=(0,\ 0)\,.}{\displaystyle A=(b\cos \gamma ,\ b\sin \gamma ),\ B=(a,\ 0),\ C=(0,\ 0)\,.}
Sử dụng công thức tính khoảng cách, ta có
{\displaystyle c={\sqrt {(a-b\cos \gamma )^{2}+(0-b\sin \gamma )^{2}}}\,.}{\displaystyle c={\sqrt {(a-b\cos \gamma )^{2}+(0-b\sin \gamma )^{2}}}\,.}
do đó
{\displaystyle {\begin{aligned}c^{2}&{}=(a-b\cos \gamma )^{2}+(-b\sin \gamma )^{2}\\c^{2}&{}=a^{2}-2ab\cos \gamma +b^{2}\cos ^{2}\gamma +b^{2}\sin ^{2}\gamma \\c^{2}&{}=a^{2}+b^{2}(\sin ^{2}\gamma +\cos ^{2}\gamma )-2ab\cos \gamma \\c^{2}&{}=a^{2}+b^{2}-2ab\cos \gamma \,.\end{aligned}}}{\displaystyle {\begin{aligned}c^{2}&{}=(a-b\cos \gamma )^{2}+(-b\sin \gamma )^{2}\\c^{2}&{}=a^{2}-2ab\cos \gamma +b^{2}\cos ^{2}\gamma +b^{2}\sin ^{2}\gamma \\c^{2}&{}=a^{2}+b^{2}(\sin ^{2}\gamma +\cos ^{2}\gamma )-2ab\cos \gamma \\c^{2}&{}=a^{2}+b^{2}-2ab\cos \gamma \,.\end{aligned}}}
Công thức này sử dụng được cả trường hợp tam giác nhọn và tam giác tù.
Hình 4 – Tam giác nhọn và đường cao
Hạ đường cao tương ứng với cạnh c như hình 4 ta có
{\displaystyle c=a\cos \beta +b\cos \alpha \,.}{\displaystyle c=a\cos \beta +b\cos \alpha \,.}
(Công thức trên vẫn đúng nếu α hoặc β là góc tù, khi đó đường cao nằm ngoài tam giác và cos α hoặc cos β mang dấu âm). Nhân hai vế với c ta được
{\displaystyle c^{2}=ac\cos \beta +bc\cos \alpha .\,}{\displaystyle c^{2}=ac\cos \beta +bc\cos \alpha .\,}
Tương tự ta có
{\displaystyle a^{2}=ac\cos \beta +ab\cos \gamma ,\,}{\displaystyle a^{2}=ac\cos \beta +ab\cos \gamma ,\,}
{\displaystyle b^{2}=bc\cos \alpha +ab\cos \gamma .\,}{\displaystyle b^{2}=bc\cos \alpha +ab\cos \gamma .\,}
Cộng vế theo vế hai phương trình sau ta có
{\displaystyle a^{2}+b^{2}=ac\cos \beta +bc\cos \alpha +2ab\cos \gamma .\,}{\displaystyle a^{2}+b^{2}=ac\cos \beta +bc\cos \alpha +2ab\cos \gamma .\,}
Trừ vế theo vế phương trình đầu ta có
{\displaystyle a^{2}+b^{2}-c^{2}=-ac\cos \beta -bc\cos \alpha +ac\cos \beta +bc\cos \alpha +2ab\cos \gamma \,}{\displaystyle a^{2}+b^{2}-c^{2}=-ac\cos \beta -bc\cos \alpha +ac\cos \beta +bc\cos \alpha +2ab\cos \gamma \,}
đơn giản còn
{\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos \gamma .\,}{\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos \gamma .\,}
Sử dụng định lý Pytago
Hình 5 – Tam giác tù ABC với đường cao BH
Trường hợp tam giác tù. Euclid chứng minh đinh lý bằng cách áp dụng Định lý Pytago cho hai tam giác vuông trong Hình 5. Đặt CH = d và BH = h, trong tam giác AHB ta có
{\displaystyle c^{2}=(b+d)^{2}+h^{2},\,}{\displaystyle c^{2}=(b+d)^{2}+h^{2},\,}
và trong tam giác CHB ta có
{\displaystyle d^{2}+h^{2}=a^{2}.\,}{\displaystyle d^{2}+h^{2}=a^{2}.\,}
Khai triển đa thức phương trình đầu tiên:
{\displaystyle c^{2}=b^{2}+2bd+d^{2}+h^{2}.\,}{\displaystyle c^{2}=b^{2}+2bd+d^{2}+h^{2}.\,}
thế phương trình thứ hai vào:
{\displaystyle c^{2}=a^{2}+b^{2}+2bd.\,}{\displaystyle c^{2}=a^{2}+b^{2}+2bd.\,}
Đây là mệnh đề 12 của Euclid trong tập 2 của bộ Cơ sở.[1] Chú ý rằng
{\displaystyle d=a\cos(\pi -\gamma )=-a\cos \gamma .\,}{\displaystyle d=a\cos(\pi -\gamma )=-a\cos \gamma .\,}
Trường hợp tam giác nhọn. Được chứng minh trong mệnh đề 13 của Euclid ngay sau mệnh đề 12: ông áp dụng Định lý Pytago cho hai tam giác vuông có được bằng cách kẻ đường cao tương ứng với một trong hai cạnh kề góc γ và đơn giản bằng nhị thức.
Hình 6 – Chứng minh bằng lượng giác trong trường hợp tam giác nhọn
Cách khác trong trường hợp tam giác nhọn. Dựa vào Hình 6 ta có:
{\displaystyle {\begin{aligned}c^{2}&{}=(b-a\cos \gamma )^{2}+(a\sin \gamma )^{2}\\&{}=b^{2}-2ab\cos \gamma +a^{2}\cos ^{2}\gamma +a^{2}\sin ^{2}\gamma \\&{}=b^{2}+a^{2}-2ab\cos \gamma ,\end{aligned}}}{\displaystyle {\begin{aligned}c^{2}&{}=(b-a\cos \gamma )^{2}+(a\sin \gamma )^{2}\\&{}=b^{2}-2ab\cos \gamma +a^{2}\cos ^{2}\gamma +a^{2}\sin ^{2}\gamma \\&{}=b^{2}+a^{2}-2ab\cos \gamma ,\end{aligned}}}
với lưu ý rằng
{\displaystyle \cos ^{2}\gamma +\sin ^{2}\gamma =1.\,}{\displaystyle \cos ^{2}\gamma +\sin ^{2}\gamma =1.\,}
Cũng từ Hình 6 ta có:
{\displaystyle \tan \alpha ={\frac {a\sin \gamma }{b-a\cos \gamma }}}{\displaystyle \tan \alpha ={\frac {a\sin \gamma }{b-a\cos \gamma }}}
Công thức này được dùng để tính một góc khi biết hai cạnh và góc xen giữa hai cạnh đó.
Chứng minh định lý cos bằng định lý Ptolemy
Vẽ đường tròn ngoại tiếp tam giác ABC. Dựng tam giác ABD bằng tam giác ABC với AD = BC và BD = AC. Hạ đường cao từ D và C, cắt AB lần lượt tại E và F. Ta có:
{\displaystyle {\begin{aligned}&BF=AE=BC\cos {\hat {B}}=a\cos {\hat {B}}\\\Rightarrow \ &DC=EF=AB-2BF=c-2a\cos {\hat {B}}.\end{aligned}}}{\displaystyle {\begin{aligned}&BF=AE=BC\cos {\hat {B}}=a\cos {\hat {B}}\\\Rightarrow \ &DC=EF=AB-2BF=c-2a\cos {\hat {B}}.\end{aligned}}}
Áp dụng định lý Ptolemy cho tứ giác nội tiếp ABCD:
{\displaystyle {\begin{aligned}&AD\times BC+AB\times DC=AC\times BD\\\Rightarrow \ &a^{2}+c(c-2a\cos {\hat {B}})=b^{2}\\\Rightarrow \ &a^{2}+c^{2}-2ac\cos {\hat {B}}=b^{2}.\end{aligned}}}{\displaystyle {\begin{aligned}&AD\times BC+AB\times DC=AC\times BD\\\Rightarrow \ &a^{2}+c(c-2a\cos {\hat {B}})=b^{2}\\\Rightarrow \ &a^{2}+c^{2}-2ac\cos {\hat {B}}=b^{2}.\end{aligned}}}
Trong tam giác cân
Trong tam giác cân, do a = b nsup> + b2 = 2a2 = 2ab}}:
{\displaystyle c^{2}=2a^{2}(1-\cos \gamma ).\;}{\displaystyle c^{2}=2a^{2}(1-\cos \gamma ).\;}
hay
{\displaystyle \cos \gamma =1-{\frac {c^{2}}{2a^{2}}}}{\displaystyle \cos \gamma =1-{\frac {c^{2}}{2a^{2}}}}
Sự tương đồng trong hình tứ diện
Cho một tứ diện với α, β, γ, δ là diện tích bốn mặt của tứ diện đó. Ký hiệu các góc nhị diện là {\displaystyle \scriptstyle {{\widehat {\beta \gamma }},}}{\displaystyle \scriptstyle {{\widehat {\beta \gamma }},}} và tương tự, ta có[2]
{\displaystyle \alpha ^{2}=\beta ^{2}+\gamma ^{2}+\delta ^{2}-2\left(\beta \gamma \cos \left({\widehat {\beta \gamma }}\right)+\gamma \delta \cos \left({\widehat {\gamma \delta }}\right)+\delta \beta \cos \left({\widehat {\delta \beta }}\right)\right).\,}{\displaystyle \alpha ^{2}=\beta ^{2}+\gamma ^{2}+\delta ^{2}-2\left(\beta \gamma \cos \left({\widehat {\beta \gamma }}\right)+\gamma \delta \cos \left({\widehat {\gamma \delta }}\right)+\delta \beta \cos \left({\widehat {\delta \beta }}\right)\right).\,}
tag: 10 đấu sao s rubik xoay trung tuyến mạch hê rông-tính trọng tâm chóp tich diên oxyz biến đổi