Thuật toán dijkstra tìm đường đi ngắn nhất

Nhắc đến giải thuật duyệt đồ thị, chắc ai học công nghệ thông tin cũng biết đến 2 thuật toán cơ bản: Depth-First Search (DFS) , Breadth-First Search (BFS).

Về mặt ý nghĩa, cả 2 thuật toán đều thực hiện trên đồ thị không có trọng số.

Thuật toán DFS cho ta tìm đường đi đến đỉnh ta muốn (có thể chưa ngắn nhất).

Còn thuật toán BFS cũng tìm đường đi đến đỉnh ta muốn nhưng là đường ngắn nhất có thể.

Trong đồ thị có trọng số, vấn đề sẽ khó hơn, nó nảy sinh ra 1 bài toán, đó là bài toán tìm đường đi ngắn nhất giữa 2 đỉnh.

Nó là bài toán rất quen thuộc với những người bắt đầu học Graph.

Để giải quyết bài toán này, đến giờ có nhiều thuật toán và các biến thể. Trong bài viết này mình sẽ chắc lọc và lựa chọn sử dụng Moore – Dijkstra.

Thuật toán Dijkstra cho phép tìm đường đi ngắn nhất từ một đỉnh s đến các đỉnh còn lại của đồ thị và chiều dài (trọng số) tương ứng.

Phương pháp của thuật toán là xác định tuần tự đỉnh có chiều dài đến s theo thứ tự tăng dần.

Thuật toán được xây dựng trên cơ sở gán cho mỗi đỉnh các nhãn tạm thời.

Nhãn tạm thời của các đỉnh cho biết cận trên của chiều dài đường đi ngắn nhất từ s đến đỉnh đó.

Nhãn của các đỉnh sẽ biến đổi trong các bước lặp, mà ở mỗi bước lặp sẽ có một nhãn tạm thời trở thành chính thức.

Nếu nhãn của một đỉnh nào đó trở thành chính thức thì đó cũng chính là chiều dài ngắn nhất của đường đi từ s đến đỉnh đó.

2. Ý tưởng và Mô tả thuật toán Dijkstra để tìm đường đi ngắn nhất

Trong phần này, chúng ta sẽ phân tích từng bước Thuật toán Dijkstra. Ở đây ta sẽ sử dụng đồ thị bên dưới để làm ví dụ để giúp bạn hiểu rõ hơn về thuật toán này.

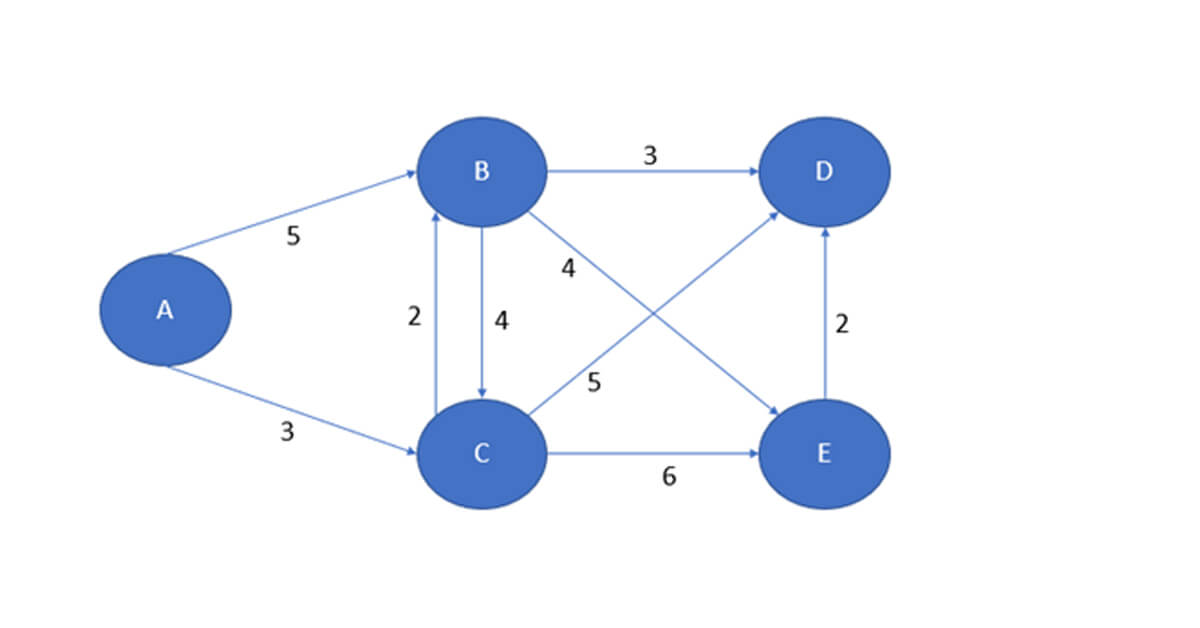
Ví dụ minh họa thuật toán tìm đường đi ngắn nhất (1)

Như bạn đã biết, thuật toán của Dijkstra là một thuật toán Greedy (Thuật toán tham lam)

Điều này có nghĩa là chúng ta sẽ đi một con đường ngắn hơn từ đỉnh này đến đỉnh kia. Thuật toán hoàn tất khi chúng ta truy cập tất cả các đỉnh của đồ thị.

Tuy nhiên, hãy cẩn thận – đôi khi khi chúng ta tìm thấy một đỉnh mới, có thể có các đường đi ngắn hơn qua nó từ một đỉnh đã truy cập đến một đỉnh đã được truy cập khác.

Chúng ta có thể xem bên dưới các bước để hoàn thành thuật toán Dijkstra.

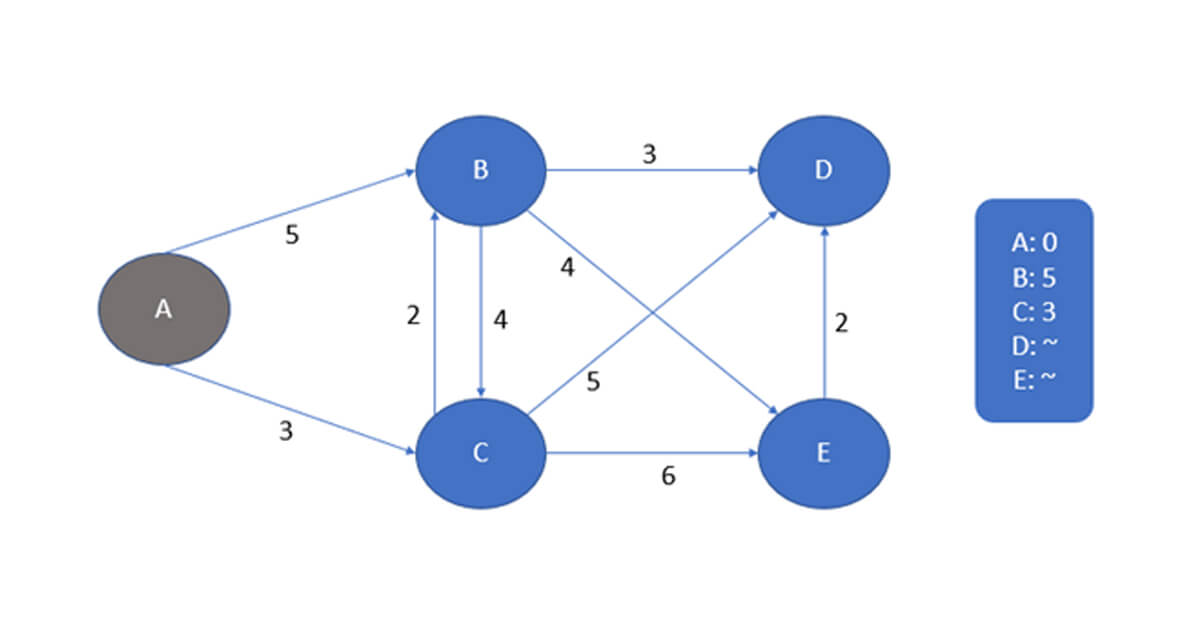
Ví dụ minh họa thuật toán tìm đường đi ngắn nhất (2)

Chúng ta có thể bắt đầu với nút A và chúng ta có 2 con đường.

Đầu tiên là từ A đến B với độ dài 5

Và từ A đến C với độ dài 3.

Vì vậy, chúng ta có thể viết trong danh sách kế bên với các đỉnh đã truy cập là 2 đỉnh mới (B, C) và trọng số để đến đó.

Sau đó, như đã nói trước đó – chúng ta sẽ chọn con đường từ A -> C.

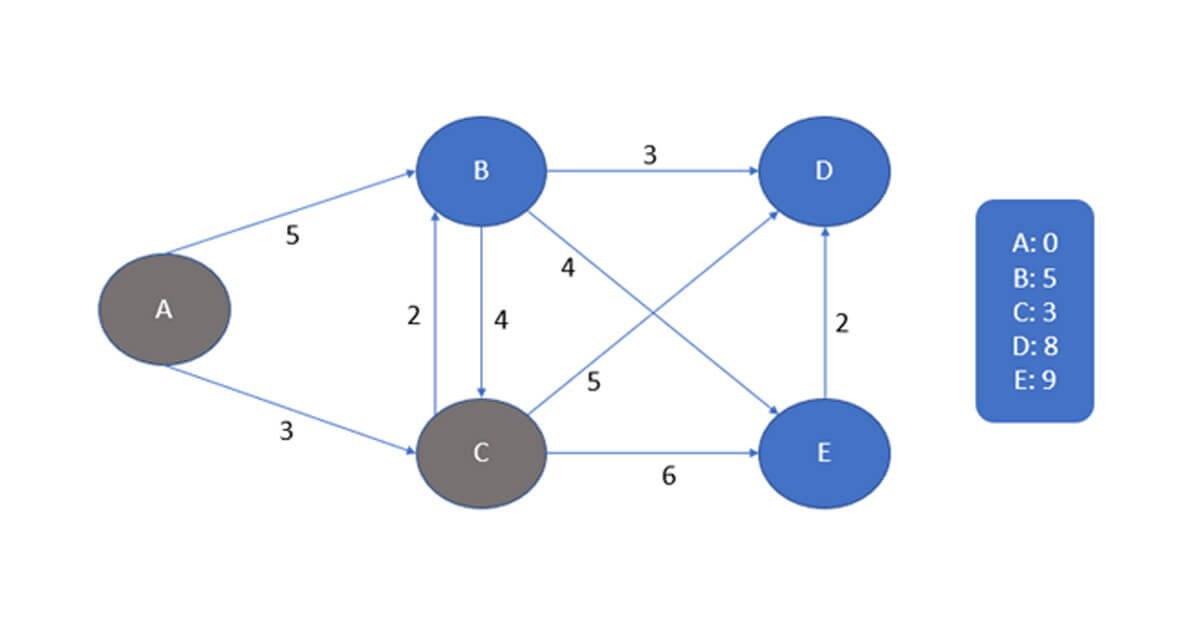
Ví dụ minh họa thuật toán tìm đường đi ngắn nhất (3)

Khi truy cập vào đỉnh C, chúng ta có thể thấy rằng có 3 đường đi khác nhau:

Con đường đầu tiên là C đến B

Con đường thứ hai là C đến D

Con đường thứ ba là C đến E

Vì vậy, hãy ghi vào danh sách hai đỉnh mới và chọn con đường ngắn nhất là C đến B.

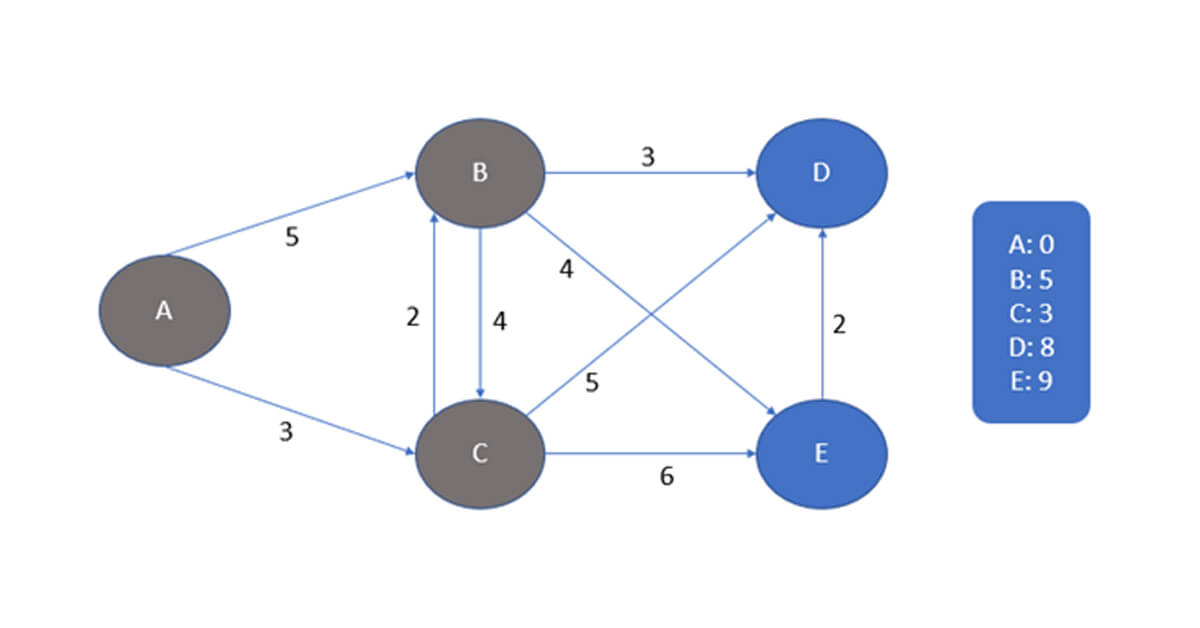
Ví dụ minh họa thuật toán tìm đường đi ngắn nhất (4)

Bây giờ tại B, chúng ta có 3 đường:

B đến D

B đến E

Và B quay lại C

Chúng ta chọn con đường ngắn nhất là B đến D và chúng ta cập nhật vào danh sách trọng số mới của các đường đi từ A đến các đỉnh khác.

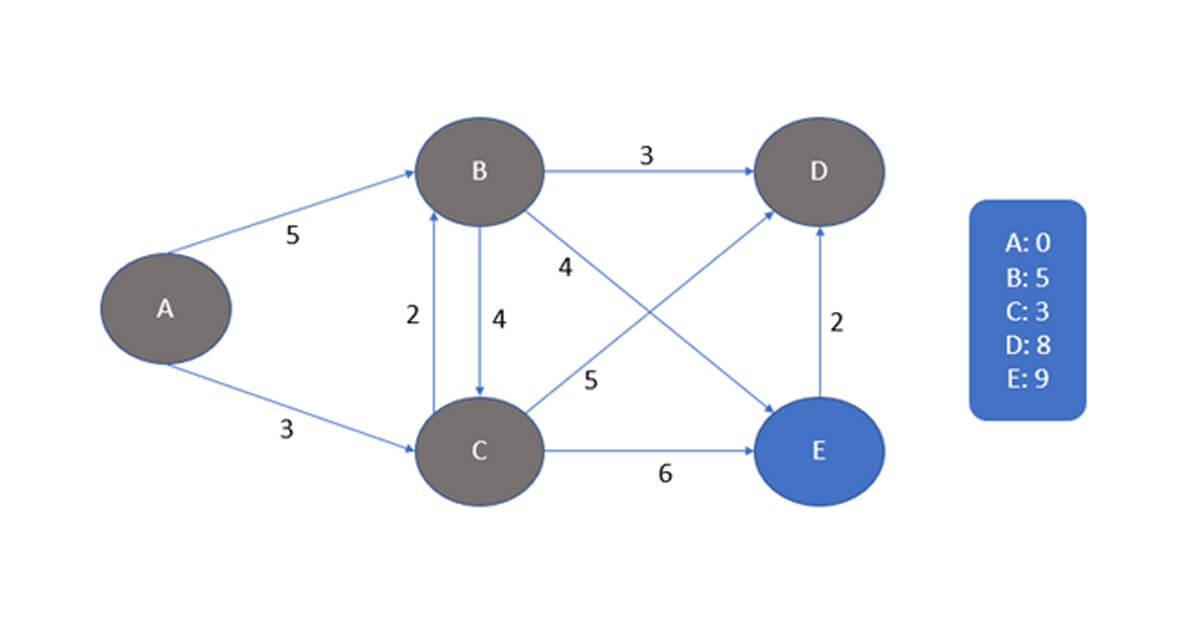
Ví dụ minh họa thuật toán tìm đường đi ngắn nhất (5)

Bây giờ như chúng ta có thể thấy không có đường đi mới nào từ D đến E.

Trong trường hợp đó, chúng ta quay lại đỉnh trước đó để kiểm tra đường đi ngắn nhất.

Bây giờ có một đường với độ dài 4 đi đến E và một đường đi đến C.

Trong trường hợp này, chúng ta chọn bất kỳ đường nào chúng ta thích.

Cuối cùng, chúng ta có thể thấy rằng bất kỳ phương án nào chúng ta đi trên đường từ A đến E đều có trọng số như nhau vì các đường đi ngắn nhất được ghi trong danh sách.

Cuối cùng, chúng ta có thể thấy tất cả các đường đi mà chúng ta đã sử dụng.

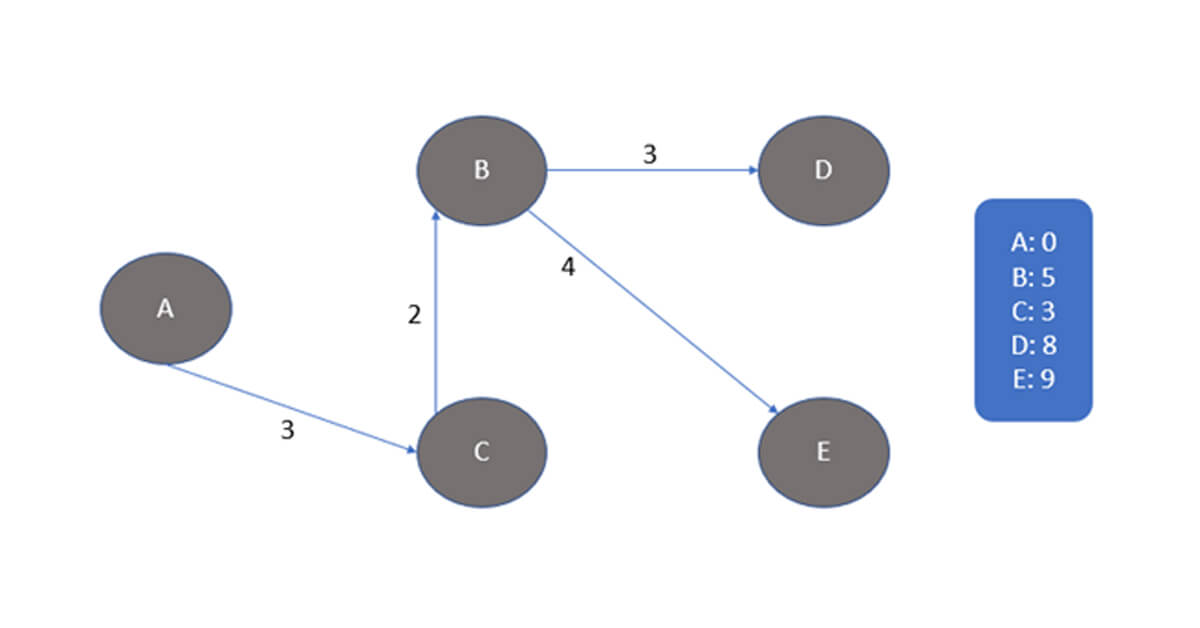
Ví dụ minh họa thuật toán tìm đường đi ngắn nhất (6)

3. Triển khai thuật toán tìm đường đi ngắn nhất trong Java

Để triển khai thuật toán tìm đường đi ngắn nhất Dijkstra, trước hết – chúng ta phải tạo các cạnh và đỉnh của biểu đồ:

File Vert.java

package dijkstra.algo;

import java.util.ArrayList;

import java.util.List;

public class Vert implements Comparable<Vert> {

private boolean visited;

private String name;

private List<Edge> List;

private double dist = Double.MAX_VALUE;

private Vert pr;

public Vert(String name) {

this.name = name;

this.List = new ArrayList<>();

}

public List<Edge> getList() {

return List;

}

public String getName() {

return name;

}

public void setName(String name) {

this.name = name;

}

public void setList(List<Edge> List) {

this.List = List;

}

public void addNeighbour(Edge edge) {

this.List.add(edge);

}

public boolean Visited() {

return visited;

}

public void setVisited(boolean visited) {

this.visited = visited;

}

public Vert getPr() {

return pr;

}

public void setPr(Vert pr) {

this.pr = pr;

}

public double getDist() {

return dist;

}

public void setDist(double dist) {

this.dist = dist;

}

@Override

public String toString() {

return this.name;

}

@Override

public int compareTo(Vert otherV) {

return Double.compare(this.dist, otherV.getDist());

}

File Edge.java

package dijkstra.algo;

public class Edge {

private double weight;

private Vert startVert;

private Vert targetVert;

public Edge(double weight, Vert startVert, Vert targetVert) {

this.weight = weight;

this.startVert = startVert;

this.targetVert = targetVert;

}

public double getWeight() {

return weight;

}

public void setWeight(double weight) {

this.weight = weight;

}

public Vert getStartVert() {

return startVert;

}

public void setStartVert(Vert startVert) {

this.startVert = startVert;

}

public Vert getTargetVert() {

return targetVert;

}

public void setTargetVert(Vert targetVert) {

this.targetVert = targetVert;

}

File PathFinder.java

package dijkstra.algo;

import java.util.ArrayList;

import java.util.Collections;

import java.util.List;

import java.util.PriorityQueue;

public class PathFinder {

public void ShortestP(Vert sourceV) {

sourceV.setDist(0);

PriorityQueue<Vert> priorityQueue = new PriorityQueue<>();

priorityQueue.add(sourceV);

sourceV.setVisited(true);

while (!priorityQueue.isEmpty()) {

Vert actualVertex = priorityQueue.poll();

for (Edge edge : actualVertex.getList()) {

Vert v = edge.getTargetVert();

if (!v.Visited()) {

double newDistance = actualVertex.getDist()
+ edge.getWeight();

if (newDistance < v.getDist()) {

priorityQueue.remove(v);

v.setDist(newDistance);

v.setPr(actualVertex);

priorityQueue.add(v);

}

actualVertex.setVisited(true);

}

public List<Vert> getShortestP(Vert targetVertex) {

List<Vert> path = new ArrayList<>();

for (Vert vertex = targetVertex; vertex != null; vertex = vertex.getPr()) {

path.add(vertex);

}

Collections.reverse(path);

return path;

}

File Dijkstra.java

package dijkstra.algo;

public class Dijkstra {

public static void main(String[] args) {

Vert vA = new Vert(“A”);

Vert vB = new Vert(“B”);

Vert vC = new Vert(“C”);

Vert vD = new Vert(“D”);

Vert vE = new Vert(“E”);

vA.addNeighbour(new Edge(3, vA, vC));

vA.addNeighbour(new Edge(5, vA, vB));

vC.addNeighbour(new Edge(2, vC, vB));

vC.addNeighbour(new Edge(6, vC, vE));

vC.addNeighbour(new Edge(5, vC, vD));

vB.addNeighbour(new Edge(4, vB, vC));

vB.addNeighbour(new Edge(3, vB, vD));

vB.addNeighbour(new Edge(4, vB, vE));

vE.addNeighbour(new Edge(2, vE, vD));

PathFinder shortestPath = new PathFinder();

shortestPath.ShortestP(vA);
System.out.println(“Khoảng cách tối thiểu từ:”);

System.out.println(“A đến B: ” + vB.getDist());

System.out.println(“A đến C: ” + vC.getDist());

System.out.println(“A đến D: ” + vD.getDist());

System.out.println(“A đến E: ” + vE.getDist());

System.out.println(“Đường đi ngắn nhất từ:”);

System.out.println(“A đến B: ” + shortestPath.getShortestP(vB));

System.out.println(“A đến C: ” + shortestPath.getShortestP(vC));

System.out.println(“A đến D: ” + shortestPath.getShortestP(vD));

System.out.println(“A đến E: ” + shortestPath.getShortestP(vE));

}

Khi chạy chương trình, kết quả ta nhận được là:

Khoảng cách tối thiểu từ:
A đến B: 5.0
A đến C: 3.0
A đến D: 8.0
A đến E: 9.0
Đương đingắn nhất từ:
A đến B: [A, B] A đến C: [A, C] A đến D: [A, C, D] A đến E: [A, C, E]

Dijkstra là thuật toán tìm đường đi có thể nói là đơn giản nhất.

Trong đồ thị, còn nhiều giải thuật tìm đường đi khác, tuỳ vào trường hợp và mục đích sử dụng mà bạn có thể dành thời gian tìm hiểu để nâng cao trình độ của mình như:

Giải bài toán đường đi ngắn nhất nguồn đơn (simple-source): Ta sẽ tìm đường đi ngắn nhất từ đỉnh nguồn v đến tất cả các đỉnh khác. Có 2 thuật toán quan trọng: Thuật toán Dijkstra (Đối với trọng số dương) và Thuật toán Bellman-Ford (Đối với trọng số bất kỳ).

Giải bài toán đường đi ngắn nhất nguồn đích (simple-destination): Ta sẽ tìm đường đi ngắn nhất trong đồ thị có hướng từ các đỉnh đến đỉnh đích v. Ta có thể giải quyết bằng cách đảo ngược hướng của đồ thị và trở thành bài toán nguồn đơn.

Giải bài toán đường đi ngắn nhất cho mọi cặp đỉnh: Ta sẽ tìm đường đi ngắn nhất giữa 2 đỉnh bất kỳ. Có 2 thuật toán quan trọng: Thuật toán Floyd-Warshall và Thuật toán Johnson.

Như vậy, qua bài hướng dẫn này bạn đã tìm hiểu được một cách để giải bài toán tìm đường đi ngắn nhất (Shortest path).

Đến đây, bạn cũng đã được học về các thuật toán Bubble sort, Selection sort, Insertion sort, Quick sort, Merge sort, Heap sort, Binary search và cả Shortest path nữa.