Trong toán học, Bài toán vận tải (tiếng Anh: transportation problem) là một dạng của bài toán quy hoạch tuyến tính. Bài toán vận tải có thể biểu diễn như một đồ thị hai phía, có hướng. Nó có thể ứng dụng vào nhiều vấn đề khác nhau. Giải thuật đơn hình trên bài toán vận tải cũng đơn giản hơn.
Giả sử có m kho hàng {\displaystyle A_{1},..,A_{m}} cùng chứa một loại hàng hóa, kho {\displaystyle A_{i}} chứa {\displaystyle a_{i}} tấn hàng. Cần vận chuyển số hàng trên đến n cửa hàng {\displaystyle B_{1},…,B_{n}}, cửa hàng {\displaystyle B_{i}} cần số hàng {\displaystyle b_{i}}. Cước phí vận chuyển một tấn hàng từ kho {\displaystyle A_{i}} đến cửa hàng {\displaystyle B_{j}} là {\displaystyle c_{ij}}. Hãy lập phương án vận chuyển sao cho tổng chi phí vận chuyển là nhỏ nhất.
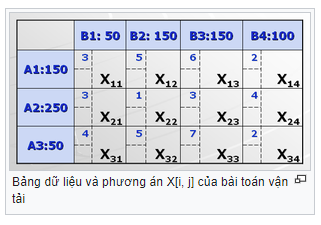
Các kho hàng được gọi là các điểm phát, các cửa hàng được gọi là các điểm thu. Ví dụ: Có 3 điểm phát và 4 điểm thu, số hàng ở các điểm phát, nhu cầu ở các điểm thu, cước phí vận chuyển cho trong bảng sau:
Bảng trên đây được gọi là bảng vận tải.
Phương án vận chuyển
Mỗi phương án vận chuyển là một ma trận X = {\displaystyle \left[x_{ij}\right]}, trong đó {\displaystyle x_{ij}} là số hàng hóa chuyển từ Ai đến Bj. ({\displaystyle x_{ij}\geq 0})
Chi phí vận chuyển của phương án X là:
-
- {\displaystyle G(X)=\sum _{i=1}^{m}\sum _{j=1}^{n}c_{ij}.x_{ij}}
Hệ ràng buộc
Để một phương án thực sự là chấp nhận được cho bài toán vận tải, các giá trị {\displaystyle x_{i,j}} phải thỏa mãn các ràng buộc đối với các điểm phát (ràng buộc dòng) là
- {\displaystyle \sum _{j=1}^{n}x_{ij}=a_{i}\,} với mọi i=1,..,m.
và các ràng buộc với các điểm thu (ràng buộc cột)
- {\displaystyle \sum _{i=1}^{m}x_{ij}=b_{j}\,} với mọi j=1,..,n.
Như vậy bài toán vận tải là bài toán QHTT dạng chính tắc với m{\displaystyle \times }n biến, hàm mục tiêu G(X) cần cực tiểu và m+n ràng buộc.
Cân bằng cung cầu
- Tổng số hàng dự trữ ở m điểm phát (cung) là {\displaystyle \sum _{i=1}^{m}a_{i}}, tổng số nhu cầu của n điểm thu (cầu)là {\displaystyle \sum _{j=1}^{n}b_{j}}. Nếu “cung” và “cầu” bằng nhau ta nói rằng cân bằng cung cầu.
- Nếu cung nhiều hơn cầu {\displaystyle \sum _{i=1}^{m}a_{i}\,>\,\sum _{j=1}^{n}b_{j}} thì một số hàng hóa sẽ được để lại ở các điểm phát. Ta biểu diễn việc này bằng cách bổ sung một điểm thu giả {\displaystyle B_{n+1}} với cước phí {\displaystyle c_{i,n+1}=0} với mọi i=1,…,n.
- Nếu cầu nhiều hơn cung {\displaystyle \sum _{i=1}^{m}a_{i}\,<\,\sum _{j=1}^{n}b_{j}} thì một số hàng hóa sẽ thiếu cho các điểm thu. Ta biểu diễn việc này bằng cách bổ sung một điểm phát giả {\displaystyle A_{m+1}} với cước phí {\displaystyle c_{m+1,j}=0} với mọi j=1,…,m.
- Như vậy bài toán vận tải luôn được đưa về bài toán thỏa mãn điều kiện cân bằng cung cầu.
Tag: giải pháp thế vị quản trị sản xuất quy giảng làm








![{\displaystyle \left[x_{ij}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9de5b3c49d6ba10dddcd553441e872a6aaa7ec3c)














