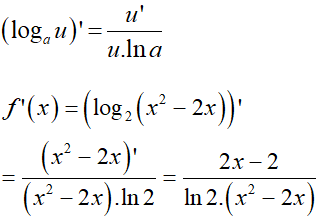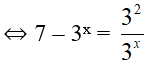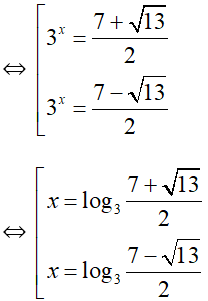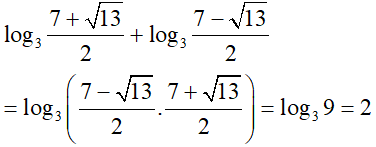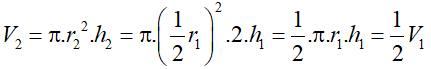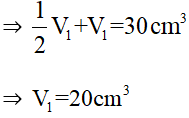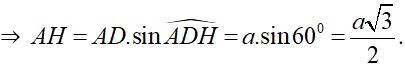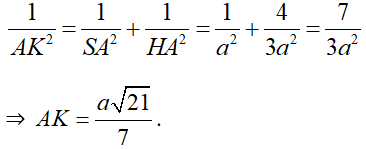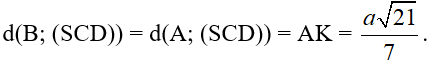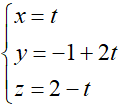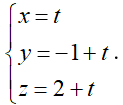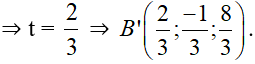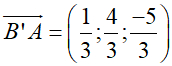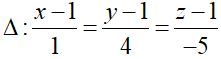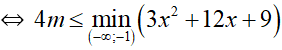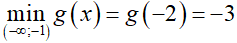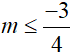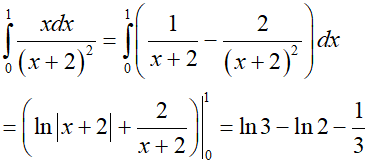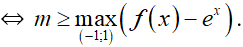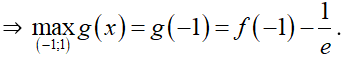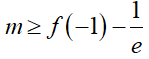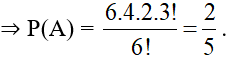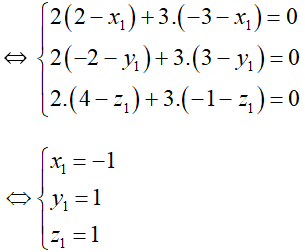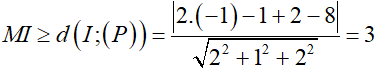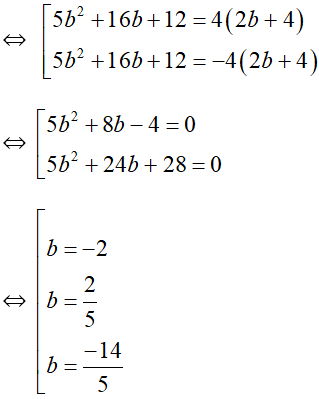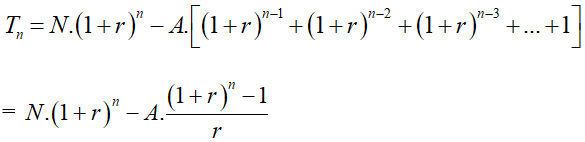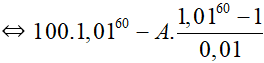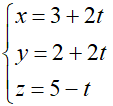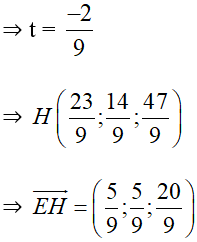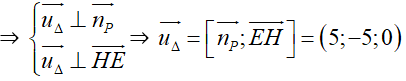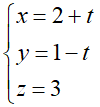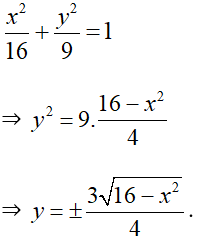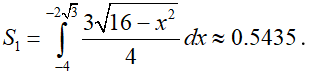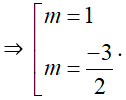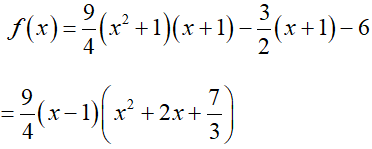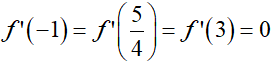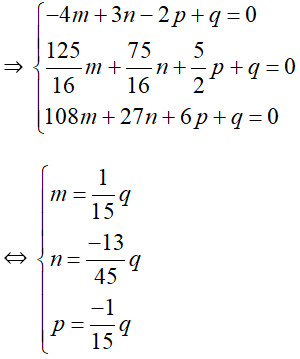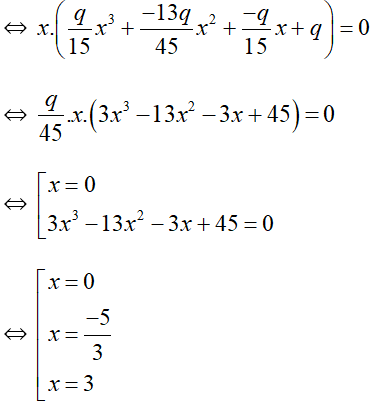Đề thi minh họa môn toán 2019

 Đề thi minh họa môn toán 2019

 Câu 1:

 Thể tích khối lập phương cạnh 2a là: V = (2a)³ = 8a³.

 Câu 2:

 Nhìn vào bảng biến thiên ta thấy hàm số đạt giá trị cực đại tại x = 2 và giá trị cực đại bằng 5.

 Câu 3:

 

 Câu 4:

 Hàm số đồng biến ⇔ đồ thị hàm số đi lên

 Quan sát đồ thị thấy hàm số đồng biến trên (–1; 0) và (1; +∞)

 Câu 5:

 Áp dụng công thức log_a(b₁b₂) = log_ab₁ + log_ab₂ và log_ab^α = α.log_ab ta có: log(ab²) = log a + log b² = log a + 2.log b

 Câu 6:

 Ta có:

 

 Câu 7:

 Theo công thức, thể tích khối cầu bán kính a bằng: 

 Câu 8:

 Tập xác định: D = R.

 log₂(x² – x + 2) = 1

 ⇔ x² – x + 2 = 2

 ⇔ x² – x = 0

 ⇔ x(x – 1) = 0

 

 Vậy tập nghiệm của phương trình là {0 ; 1}

 Câu 9:

 Mặt phẳng (Oxz) có phương trình y = 0.

 Câu 10:

 Ta có :

 

 Câu 11:

 Thay lần lượt tọa độ các điểm vào phương trình đường thẳng d ta thấy chỉ có điểm P(1; 2; 3) thỏa mãn:

 

 Câu 12:

 Ta có công thức 

 Câu 13:

 Ta có: u_n = u₁ + (n – 1).d

 Do đó: u₄ = u₁ + 3d = 2 + 3.5 = 17.

 Câu 14:

 Điểm biểu diễn số phức z = ai + b có tọa độ (a ; b)

 Điểm biểu diễn số phức z = –1 + 2i có tọa độ (–1 ; 2) và là điểm Q.

 Câu 15:

 Từ hình dạng đồ thị ta thấy đây là đồ thị hàm số dạng 

 Đồ thị có đường tiệm cận đứng 

 Đồ thị có đường tiệm cận ngang 

 Chỉ có đồ thị hàm số 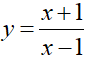 thỏa mãn điều kiện trên.

 Câu 16:

 Quan sát đồ thị ta thấy trên [–1 ; 3]

 + Hàm số đạt giá trị lớn nhất tại x = 3, giá trị lớn nhất M = 3.

 + Hàm số đạt giá trị nhỏ nhất tại x = 2, giá trị nhỏ nhất m = –2.

 Vậy M – m = 5.

 Câu 17:

 Xét : f’(x) = 0

 ⇔ x(x – 1)(x + 2)³ = 0

 

 Ta có bảng biến thiên:

 

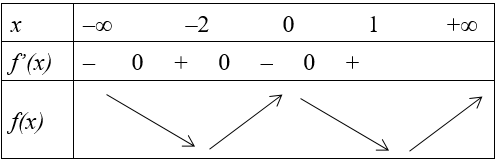
 Dựa vào bảng biến thiên thấy hàm số có ba điểm cực trị

 Câu 18:

 Ta có: 2a + (b + i).i = 1 + 2i

 ⇔ 2a + bi + i2 = 1 + 2i

 ⇔ 2a – 1 + bi = 1 + 2i     (Vì i² = –1)

 

 Câu 19:

 Bán kính mặt cầu: 

 Phương trình mặt cầu tâm I(1; 1; 1) và bán kính R = √5 là:

 (x – 1)² + (y – 1)² + (z – 1)² = 5.

 Câu 20:

 Ta có:

 

 Câu 21:

 Giải phương trình z² – 3z + 5 = 0 ta có hai nghiệm:

 

 Do đó:

 

 Câu 22:

 Ta có: (P) nhận n→ = (1; 2; 2) là một vtpt

 (Q) cũng nhận n→ = (1; 2; 2) là một vtpt

 ⇒ (P) // (Q)

 ⇒ d((P); (Q)) = d(M; (Q)) với M là một điểm bất kì thuộc mặt phẳng (P).

 Chọn M(0 ; 0 ; 5).

 

 Câu 23:

 Tập xác định: D = R.

 3^{x2 – 2x} < 27

 ⇔ x² – 2x < 3

 ⇔ x² – 2x – 3 < 0

 ⇔ (x + 1)(x – 3) < 0

 ⇔ –1 < x < 3 .

 Vậy tập nghiệm của bất phương trình là (–1; 3).

 Câu 24:

 Phần hình phẳng gạch chéo trong hình vẽ là phần hình giới hạn bởi đồ thị hàm số y = x² – 2x – 1 , đồ thị hàm số y = –x² + 3 và các đường thẳng x = –1, x = 2.

 Vậy diện tích phần hình đó là:

 

 Mà trong (–1; 2), 2x² – 2x – 4 < 0 nên |2x² – 2x – 4| = –2x² + 2x + 4.

 Do đó : 

 Câu 25:

 + Đáy của khối nón là hình tròn có bán kính R = a.

 ⇒ Diện tích mặt đáy của khối nón là: S = π.a2.

 + Gọi chiều cao của khối nón là h

 Ta có: đường sinh bằng 2a ⇒ l = 2a

 Mà: l² = h² + R² ⇒ h² = l² – R² = 3a² ⇒ h = a√3 .

 Vậy thể tích khối nón là 

 Câu 26:

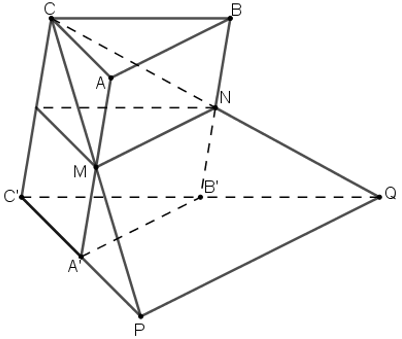
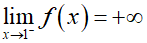
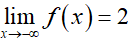
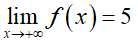
 Ta có :  nên x = 1 là tiệm cận đứng của đồ thị hàm số.

  nên y = 2 là một tiệm cận ngang của đồ thị hàm số.

  nên y = 5 là một tiệm cận ngang của đồ thị hàm số.

 Vậy hàm số tổng ba tiệm cận đứng và ngang.

 Câu 27:

 

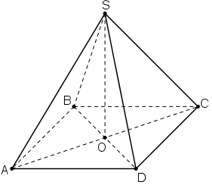
 S.ABCD là khối chóp tứ giác đều nên SO ⊥ (ABCD) nên .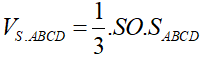

 + SABCD = 4a².

 

 ΔSOA vuông tại O .

 Vậy thể tích khối chóp bằng .

 Câu 28:

 Ta có :

 

 Câu 29:

 2.f(x) + 3 = 0 

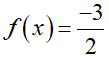
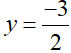
 Số nghiệm thực của phương trình 2.f(x) + 3 = 0 là số nghiệm thực của phương trình  và bằng số giao điểm của đường thẳng  và đồ thị hàm số y = f(x)

 Dựa vào bảng biến thiên ta thấy đường thẳng 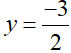 sẽ cắt đồ thị hàm số tại 4 điểm.

 Vậy phương trình có bốn nghiệm

  

 Giải đề minh họa toán 2019

  

 Câu 30:

 

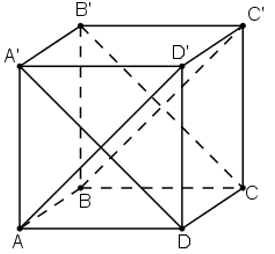
 Để tính góc giữa hai mặt phẳng, ta góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.

 Ta có : ABCD.A’B’C’D’ là hình lập phương

 ⇒ A’B’ ⊥ (AA’D’D)

 ⇒ A’B’ ⊥ AD’.

 Mà: A’D ⊥ AD’

 A’B’ cắt A’D

 ⇒ (A’B’CD) ⊥ AD’        (1)

 Chứng minh tương tự ta có: (ABC’D’) ⊥ A’D         (2)

 ⇒ ((A’B’CD) ; (ABC’D’)) = (AD’; A’D).

 Mà AA’D’D là hình vuông nên AD’ ⊥ AD’ ⇒ (AD’; A’D) = 90⁰

 ⇒ ((A’B’CD) ; (ABC’D’)) = 90⁰.

 Câu 31:

 Xét phương trình : log₃(7 – 3³) = 2 – x (1)

 Điều kiện xác định: 7 – 3^x > 0

 (1) ⇔ 7 – 3^x = 3^2-x

 

 ⇔ 7.3^x – (3^x)² = 3²

 ⇔ 3^2x – 7.3^x + 9 = 0

 

 Tổng các nghiệm của phương trình là:

 

 Câu 32:

 Thể tích khối trụ bằng: V = πr²h, trong đó r là bán kính đáy khối trụ, h là chiều cao khối trụ.

 Do đó, ta có:

 

 Mà V₂ + V₁ = 30 cm³

 

 Câu 33:

 Ta có:

 

 + Tính 

 Đặt 

 

 Vậy

 

 Câu 34:

 

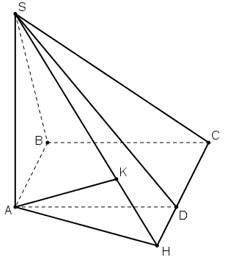
 AB // CD ⇒ AB // (SCD) ⇒ d(B; (SCD)) = d(A; (SCD))

 Kẻ AH ⊥ CD, AK ⊥ SH.

 + Chứng minh d(A; (SCD)) = AK.

 Ta có: SA ⊥ (ABCD) ⇒ SA ⊥ CD

 Mà AH ⊥ CD

 ⇒ CD ⊥ (SAH) ⇒ CD ⊥ AK.

 Mà AK ⊥ SH

 ⇒ AK ⊥ (SCD)

 Vậy d(A; (SCD)) = AK.

 + Tính AK:

 Hình thoi ABCD có 

 Xét ΔADH vuông tại H có 

 

 Xét ΔSAH vuông tại A, đường cao AK có:

 

 Vậy 

 Câu 35:

 + Tìm giao điểm của (d) và (P).

 Phương trình tham số của d: 

 Gọi A(t; –1 + 2t; 2 – t) là giao điểm của (d) và (P)

 ⇒ t + 2t – 1 + 2 – t – 3 = 0 ⇒ t = 1.

 Vậy A(1; 1; 1).

 + Lấy điểm B(0; –1; 2) ∈ (d). Tìm B’ là hình chiếu của B trên (P).

 Gọi d’ là đường thẳng đi qua B và vuông góc với (P)

 ⇒ d’ nhận u→ = n_P→ = (1; 1; 1) là một vtcp

 ⇒ Phương trình d’: 

 B’(t; –1 + t; 2 + t) là hình chiếu của B trên (P) ⇒ B’ = (d’) ∩ (P)

 ⇒ t + t – 1 + t + 2 – 3 = 0 

 + Gọi Δ là hình chiếu của (d) trên (P).

 Δ là đường thẳng qua A và B’

 

 ⇒ Δ nhận u→ = (1; 4; -5) là một vtcp

 Δ đi qua A(1; 1; 1) nên 

 Câu 36:

 Ta có: y’ = –3×2 – 12x + 4m – 9.

 Hàm số nghịch biến trên (–∞; –1)

 ⇔ y’ ≤ 0 với ∀ x ∈ (–∞; –1)

 ⇔ –3×2 – 12x + 4m – 9 ≤ 0 ∀ x ∈ (–∞; –1)

 ⇔ 4m ≤ 3×2 + 12x + 9 ∀ x ∈ (–∞; –1)

 

 + Xét g(x) = 3×2 + 12x + 9

 g’(x) = 6x + 12

 g’(x) = 0 ⇔ x = –2.

 

 Vậy 4m ≤ –3 hay 

 Câu 37:

 Đặt z = a + bi ⇒ z− = a – bi.

 (z + 2i)(z− + 2)

 = (a + bi + 2i)(a – bi + 2)

 = [a + (b + 2)i].[(a + 2) – bi]

 = a(a + 2) + b(b + 2) + [(a + 2)(b + 2) – ab].i

 (z + 2i)(z− + 2) là số thuần ảo

 ⇔ a(a + 2) + b(b + 2) = 0

 ⇔ a² + 2a + b² + 2b = 0

 ⇔ (a + 1)² + (b + 1)² = 2.

 Vậy tập hợp các điểm biểu diễn của z là đường tròn (x + 1)² + (y + 1)² = 2 có tâm (–1; –1).

 Câu 38:

 

 ⇒ a = –1/3, b = –1, c = 1

 ⇒ 3a + b + c = –1.

 Câu 39:

 Ta có:

 f(x) < e^x + m ∀ x ∈ (–1; 1)

 ⇔ m > f(x) – e^x ∀ x ∈ (–1; 1)

 

 Xét g(x) = f(x) – e^x.

 g’(x) = f’(x) – e^x.

 Dựa vào bảng biến thiên ta thấy f’(x) < 0 với ∀ x ∈ (–1; 1)

 ⇒ g’(x) = f’(x) – e^x < 0 với ∀ x ∈ (–1; 1)

 ⇒ g(x) nghịch biến trên (–1; 1)

 

 Vậy 

 Câu 40:

 + Không gian mẫu: n(Ω) = 6!

 Gọi A : “Mỗi học sinh nam đều ngồi đối diện với một học sinh nữ”

 Chọn chỗ cho học sinh nữ đầu tiên có 6 (cách)

 Chọn chỗ cho học sinh nữ thứ hai (Không ngồi đối diện với học sinh nữ đầu) có 4 (cách)

 Chọn chỗ cho học sinh nữ thứ ba (không ngồi đối diện với học sinh nữ đầu và thứ 2) có 2 (cách)

 Xếp 3 học sinh nam vào ba chỗ còn lại có 3! (cách)

 ⇒ n(A) = 6.4.2.3!

 

 Câu 41:

 Gọi I(x₁; y₁; z₁) là điểm thỏa mãn 2IA→ + 3IB→ = 0→

 ⇔ 2.(2 – x₁; –2 – y₁; 4 – z₁) + 3.(–3 – x₁; 3 – y₁; –1 – z₁) = (0; 0; 0)

 

 ⇒ I(–1; 1; 1) ⇒ IA² = 27 , IB² = 12

 Ta có:

 2.MA² + 3.MB² = 2.MA→ + 3.MB→

 2.(MI→ + IA→)² + 3.(MI→ + IB→)²

 = 5.MI² + 2.MI→.(2.IA→ + 3.IB→) + 2.IA² + 3.IB²

 = 5.MI² + 0 + 2.27 + 3.12

 = 5.MI² + 90.

 Mà ta có: 

 Do đó 2.MA² + 3.MB² ≥ 5.3² + 90 = 135.

 Câu 42:

 Giả sử z = a = bi

 ⇒ z− = a – bi

 Ta có: |z|² = 2.|z + z−| + 4

 ⇔ |z²| = 2.|2a| + 4

 ⇔ a² + b² = 4|a| + 4    (1)

 |z – 1 – i| = |z – 3 + 3i|

 ⇔ |(a – 1) + (b – 1)I| = |(a – 3) + (b – 3)i|

 ⇔ (a – 1)² + (b – 1)² = (a – 3)² + (b + 3)²

 ⇔ a – 2b – 4 = 0

 ⇔ a = 2b + 4     (2)

 Thế (2) vào (1) ta được:

 (2b + 4)² + b² = 4.|2b + 4| + 4

 ⇔ 5b² + 16b + 12 = 4.|2b + 4|

 

 Vậy có ba số phức thỏa mãn điều kiện giả thiết.

 Câu 43:

 Đặt t = sin x.

 x ∈ (0; π) ⇒ t ∈ (0; 1].

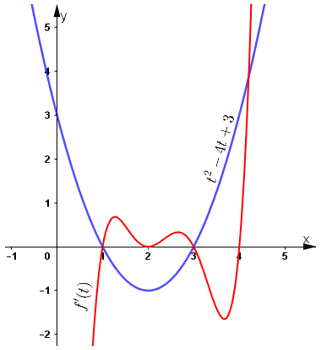
 Phương trình f (sin x) = m có nghiệm thuộc khoảng (0; π)

 ⇔ phương trình f(t) = m có nghiệm t ∈ (0; 1]

 Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y = f(t) và đường thẳng y = m.

 Dựa vào đồ thị hàm số ta thấy: phương trình f(t) = m có nghiệm t ∈ (0; 1] khi đường thẳng y = m cắt đồ thị hàm số f trên (0; 1] hay –1 ≤ m < 1.

 Câu 44:

 Gọi N là số tiền vay ban đầu, r là lãi suất hàng tháng, A là số tiền ông A hoàn nợ hàng tháng.

 + Số tiền còn nợ ngân hàng sau tháng thứ nhất:

 T₁ = N.(1 + r) – A

 + Số tiền còn nợ ngân hàng sau tháng thứ hai:

 T₂ = T₁.(1 + r) – A = N.(1 + r)² – A.(1 + r) – A

 + Số tiền còn nợ ngân hàng sau tháng thứ ba:

 T₃ = T₂(1 + r) – A = N.(1 + r)³ – A.(1 + r)² – A(1 + r) – A

 …

 + Số tiền nợ ngân hàng sau tháng thứ n:

 

 Áp dụng vào bài toán với N = 100 triệu đồng, r = 0,01.

 Sau 5 năm (60 tháng), ông A trả hết nợ nên ta có:

 T₆₀ = 0

 

 A ≈ 2,22

 Câu 45:

 Mặt cầu (S): (x – 3)² + (y – 2)² + (z – 5)² = 36 có tâm I(3; 2; 5) và bán kính R = 6.

 IE = √6 < R nên E nằm trong mặt cầu.

 (P) có vecto pháp tuyến n_P→ = (2; 2; -1)

 + Tìm hình chiếu H của I trên mặt phẳng (P).

 Đường thẳng qua I và vuông góc với (P): 

 H là hình chiếu của I trên (P) nên H(3 + 2t; 2 + 2t; 5 – t).

 H ∈ (P) ⇒ 2(3 + 2t) + 2(2 + 5t) – 5 + t – 3 = 0

 

 + (Δ) đi qua E, nằm trong (P) và cắt (S) tại 2 điểm có khoảng cách nhỏ nhất

 ⇔ Δ đi qua E, nằm trong (P) và Δ ⊥ EH.

 

 ⇒ Δ cũng nhận u→ = (1; -1; 0) là vectơ chỉ phương .

 Vậy phương trình đường thẳng cần tìm: 

 Câu 46:

 

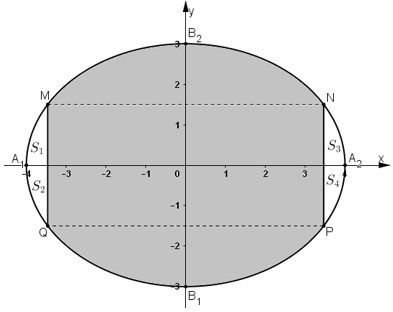
 (E) có A₁A₂ = 8m ⇒ 2a = 8 ⇒ a = 4.

 (E) có B₁B₂ = 6m ⇒ 2b = 6 ⇒ b = 3.

 Phương trình chính tắc của elip:

 

 M ∈ (E), 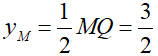 ⇒ x_M = -2√3 (Vì x_M < 0).

 Đường thẳng MQ: x = -2√3 .

 S₁ là phần diện tích được giới hạn bởi (E), trục Ox và đường thẳng MQ.

 Do đó 

 Diện tích phần không bị tô màu là: S₁ + S₂ + S₃ + S₄ ≈ 2,174

 Diện tích cả elip là: S = π.a.b = 12π

 Diện tích phần được tô màu là: 12π – 2,174 ≈ 35,525.

 Chi phí để sơn biển quảng cáo là:

 2,174.100000 + 35,525.200000 ≈ 7322000

 Câu 47:

 

 Đặt V = V_{ABC.A’B’C’}

 Ta có: 

 

 Câu 48:

 y = 3.f(x + 2) – x³ + 3x đồng biến

 ⇔ y’ = 3. f’(x + 2) – 3x² + 3 > 0

 ⇔ f’(x + 2) – x² + 1 > 0    (1)

 Đặt t = x + 2 ⇒ x = t – 2

 (1) trở thành f’(t) > (t – 2)² – 1

 ⇔ f’(t) > t² – 4t + 3.

 Dựa vào bảng biến thiên ta có đồ thị:

 

 Nhìn vào đồ thị thấy:

 f’(t) > t² – 4t + 3

 ⇔ 1 < t < 3 hoặc t > 4

 ⇔ -1 < x < 1 hoặc x > 2

 Trong các đáp án trên chỉ có C. thỏa mãn.

 Câu 49:

 Ta có: m²(x⁴ – 1) + m(x² – 1) – 6(x – 1) ≥ 0        ∀ x ∈ R

 ⇔ m²(x² + 1)(x – 1)(x + 1) + m(x – 1)(x + 1) – 6(x – 1) ≥ 0        ∀ x ∈ R

 ⇔ (x – 1)[m²(x² + 1)(x + 1) + m(x + 1) – 6] ≥ 0 ∀ x ∈ R        (1)

 + Với m = 0, (1) ⇔ -6(x – 1) ≥ 0 ∀ x ∈ R (Loại)

 + Với m ≠ 0. Đặt f(x) = m²(x² + 1)(x + 1) + m(x + 1) – 6.

 ⇒ x = 1 phải là nghiệm của f(x)

 ⇒ 4m² + 2m – 6 = 0

 

 Nếu m = 1, thì f(x) = (x² + 1)(x + 1) + (x + 1) – 6

 = x³ + x² + 2x – 4

 = (x – 1)(x² + 2x + 4)

 (1) trở thành (x – 1)² (x² + 2x + 4) ≥ 0    ∀ x ∈ R (Thỏa mãn)

 Nếu m = -3/2 thì

 

 (1) trở thành 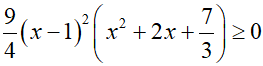 ∀ x ∈ R (Thỏa mãn)

 Vậy có hai giá trị của m thỏa mãn là m = 1 và m = -3/2 . Tổng của chúng bằng -1/2

 Câu 50:

 f(x) = mx⁴ + nx³ + px² + qx + r

 ⇒ f’(x) = 4mx³ + 3nx² + 2px + q.

 Dựa vào đồ thị hàm số y = f’(x) ta thấy: 

 

 Xét f(x) = r

 ⇔ mx⁴ + nx³ + px² + qx + r = r

 ⇔ mx⁴ + nx³ + px² + qx = 0

 ⇔ x.(mx³ + nx² + px + q) = 0

 

 Vậy phương trình f(x) = r có ba nghiệm

  

  

  

 tag: chữa tiết an dđáp file word phát triển bộ giáo dục hướng dẫn violet dđề ma trận
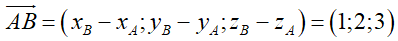
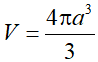
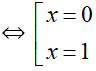
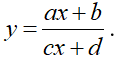
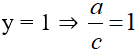
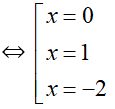
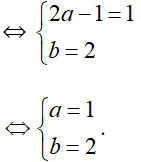
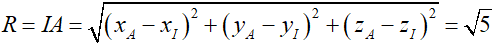
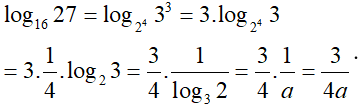
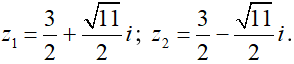
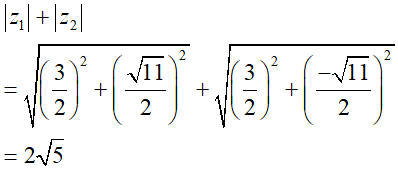
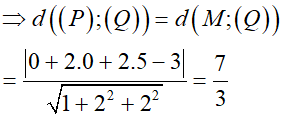
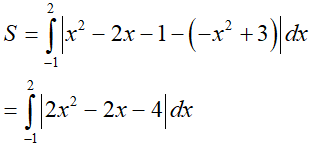
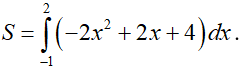
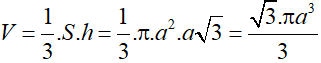
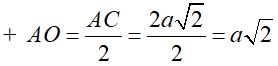
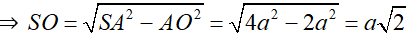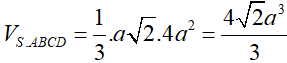