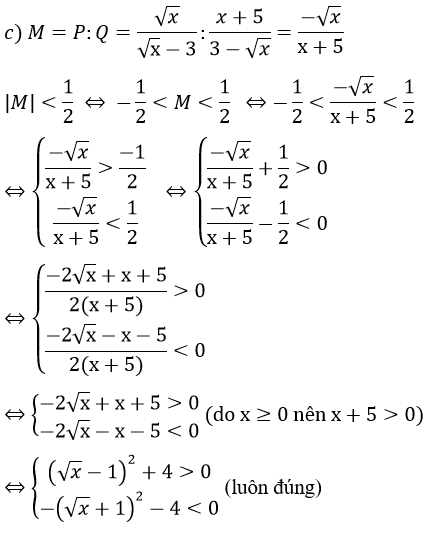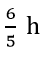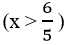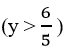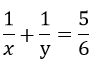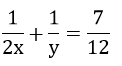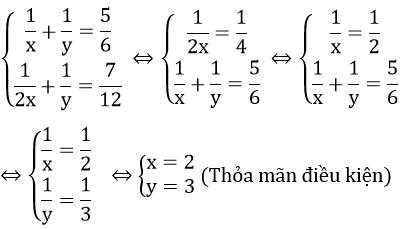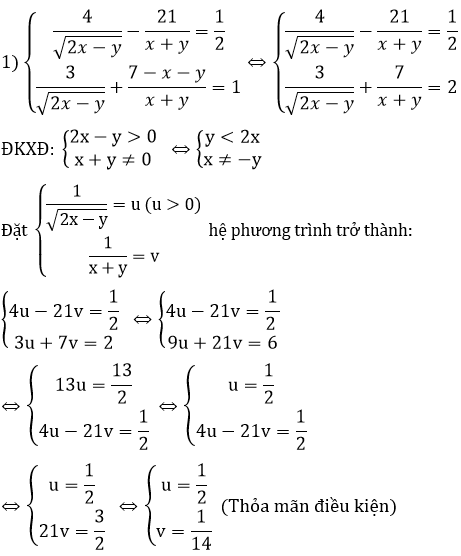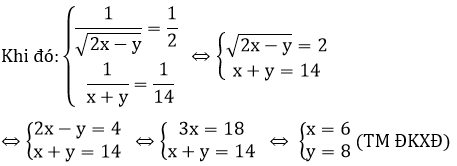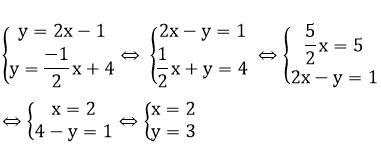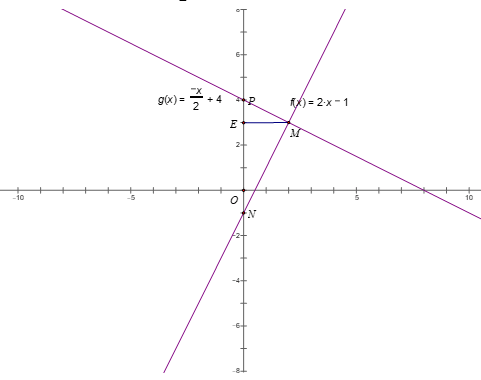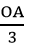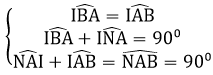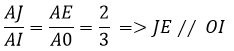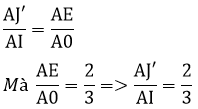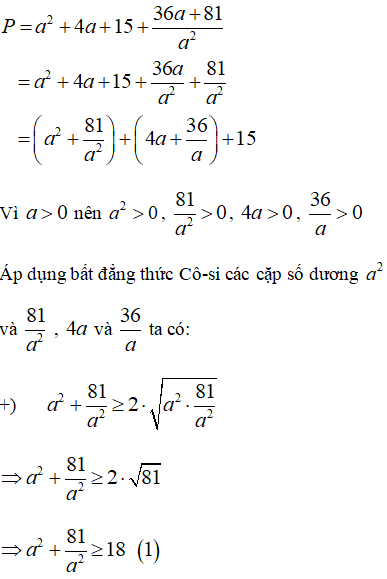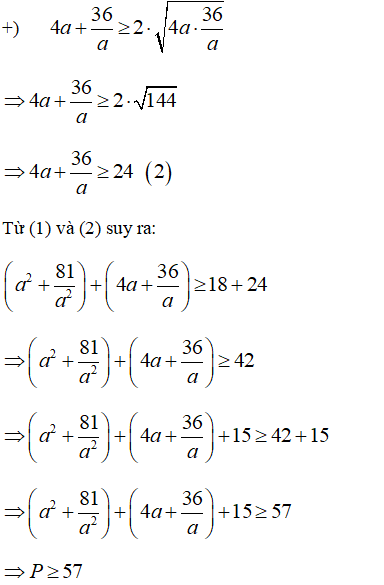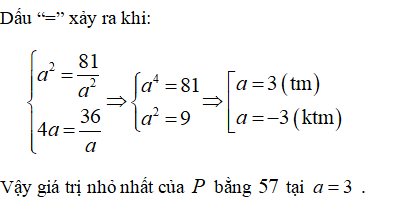Phần I. Trắc nghiệm (2 điểm)
Câu 1 : Điều kiện xác định của biểu thức P = 2018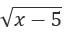
A.x = 5 B.x ≠ 5 C.x ≤ 5 D.x ≥ 5
Câu 2: Trong mặt phẳng tọa độ Oxy, đường thẳng 2x – y = 3 đi qua điểm:
A. (0; -3) B. (2; 2) C. ( 1; 3) D. (5; 0)
Câu 3: Cho hàm số y = -3x2. Kết luận nào sau đây là đúng :
B. Hàm số trên luôn nghịch biến
C. Hàm số trên đồng biến khi x > 0, nghịch biến khi x < 0
D. Hàm số trên đồng biến khi x < 0, nghịch biến khi x > 0
Câu 4: Điều kiện để hàm số y = (- m + 3) x – 7 đồng biến trên R là:
A. m = 3 B. m ≤ 3 C. m ≥ 3 D. x ≠ 3
Câu 5 : Trong các phương trình sau, phương trình nào có tích hai nghiệm bằng -5
A. x2 – 3 x – 5 = 0 B. x2 – 3 x + 5 = 0
C. x2 + 3 x + 5 = 0 D. –x2 – 3 x – 5 = 0
Câu 6: Cho tam giác ABC vuông tại A có đường cao AH có BH = 6 cm; CH = 12 cm. Độ dài cạnh góc vuông AB là:
A.6cm B.6√2 cm C.6√3 cm D.12 cm
Câu 7: Cung AB của đường tròn (O; R) có số đo là 60o. Khi đó diện tích hình quạt AOB là:
Câu 8: Tứ giác MNPQ nội tiếp đường tròn khi:
A.∠MNP + ∠NPQ = 180o B.∠MNP = ∠MPQ
C. MNPQ là hình thang cân D. MNPQ là hình thoi
Phần II. Tự luận
a) Tìm điều kiện đối với a và b để biểu thức P có nghĩa rồi rút gọn biểu thức P
b) Khi a và b là 2 nghiệm của phương trình bậc hai x2 – 3x + 1 =0. Không cần giải phương trình này, hãy chứng tỏ giá trị của P là một số nguyên dương
a) Tìm điểm cố định của đường thẳng y = (m – 1)x + 2m – 1
b) Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d): y = mx + 1 và Parabol (P): y = 2x2. Tìm m để đường thẳng (d) đi qua điểm A (3; 7). Chứng minh rằng (d) luôn cắt (P) tại 2 điểm phân biệt C (x1, y1) và D (x2, y2). Tính giá trị của T = x1x2 + y1y2
Bài 3: (1,5 điểm) Giải các phương trình và hệ phương trình sau:
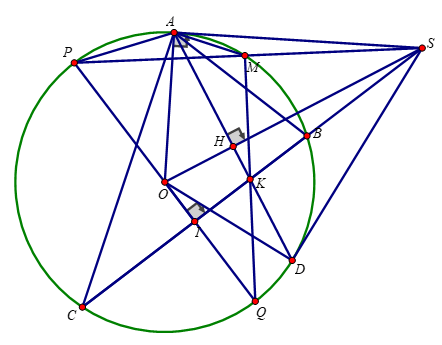
Bài 4: (3,5 điểm) Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O). Tiếp tuyến tại A của (O) cắt BC tại S. Gọi I là trung điểm của BC.
a) Chứng minh tứ giác SAOI nội tiếp
b) Vẽ dây cung AD vuông góc với SO tại H. AD cắt BC tại K. Chứng minh SD là tiếp tuyến của đường tròn (O)
d) Vẽ đường kính PQ đi qua điểm I (Q thuộc cung CD), SP cắt đường tròn (O) tại M. Chứng minh M, K, Q thẳng hàng.
Bài 5: (0,5 điểm) Cho a, b, c > 0 và a + b + c = 3. Chứng minh rằng:
Phần I. Trắc nghiệm
| 1.D | 2.A | 3.D | 4.B |
| 5.A | 6.C | 7.B | 8.C |
Phần II. Tự luận
b) a, b là 2 nghiệm của phương trình x2 – 3x + 1 =0 nên theo hệ thức Vi-ét ta có:
Vậy giá trị của P là một số nguyên dương
Gọi M (x0 ; y0) là điểm cố định mà đường thẳng y = (m – 1)x + 2m – 1 đi qua với mọi m
=> y0 = (m – 1) x0 + 2m – 1 ⇔ (x0 + 2)m – (y0 + x0 + 1)=0 (*)
Để đường thẳng y = (m – 1)x + 2m – 1 luôn đi qua M (x0 ; y0) với mọi m thì phương trình (*) nghiệm đúng với mọi m
Vậy đường thẳng y = (m – 1)x + 2m – 1 luôn đi qua M (-2; 1)
b) Để đường thẳng (d): y = mx + 1 đi qua điểm A (3; 7), thì A ∈ d :
Phương trình hoành độ giao điểm của (P) và (d) là:
2x2 = mx + 1 ⇔ 2x2 – mx – 1 = 0
Δ = m2 – 4.2.(-1) = m2 + 8 > 0
=> Phương trình có 2 nghiệm phân biệt, do đó (d) cắt (P) tại 2 điểm phân biệt
T = x1x2 + y1y2 = x1x2 + (mx1 + 1)(mx2 + 1)
= x1x2 + m(x1 + x2 ) + m2x1x2 + 1
Vậy hệ phương trình đã cho có nghiệm (x; y) = (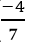
Đặt x2 = t (t ≥ 0), phương trình trở thành:
Phương trình có dạng a + b + c = 3 + 1 – 4 = 0. Do đó, phương trình có hai nghiệm
Vậy phương trình đã cho có hai nghiệm x = ± 1.
a) Ta có: BC là dây cung, I là trung điểm của BC
∠SAO = 90o (Do SA là tiếp tuyến của (O))
=> Tứ giác SAOI là tứ giác nội tiếp
b) Tam giác AOD cân tại O có OH là đường cao
=> OH cũng là trung trực của AD
∠SAB = ∠ACB (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AB)
ΔSAO vuông tại O có AH là đường cao
Từ (1), (2) và (3) => SK.SI = SB.SC
d) Ta có: ∠PMQ = 90o (Góc nội tiếp chắn nửa đường tròn)
∠SAM = ∠SPA (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AM)
=> ∠SMK = ∠SIP = 90o => MK ⊥ SP
Ta có: PS ⊥ MQ ; MK ⊥ SP => M;Q;K thẳng hàng
Áp dụng bất đẳng thức Co- si, ta được:
=> a5 + b5 + c5 + 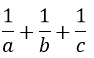
=> a2 + b2 + c2 ≥ 2 (a + b + c)-3 = 2 . 3 – 3 = 3
Vậy ta được điều phải chứng minh.
Đề thi vào 10 môn toán hà nội các năm
Bài 1: (2 điểm) Cho các biểu thức:
c) Đặt M = P : Q. Tìm x để |M| <
Bài 2: (2 điểm) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình: Hai vòi nước cùng chảy vào một bể nước cạn (không có nước) trong 1 giờ 12 phút thì đầy bể. Nếu mở vòi thứ nhất chảy trong 30 phút và vòi thứ hai chảy trong 1 giờ thì được 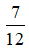
2) Cho hai hàm số: y = 2x – 1 và y = 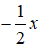
a) Tìm tọa độ giao điểm M của đồ thị hai hàm số trên
b) Gọi N, P lần lượt là giao điểm của hai đồ thị trên với trục Oy. Tính diện tích ΔMNP
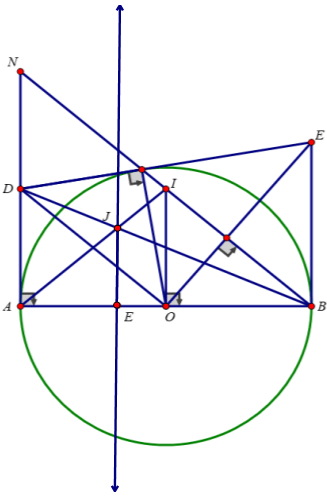
Bài 4: (3,5 điểm) Cho đường tròn (O ; R) đường kính AB và điểm M bất kì thuộc đường tròn (M ≠ A, B) . Kẻ tiếp tuyến tại A của đường tròn, tiếp tuyến này cắt tia BM ở N. Tiếp tuyến của đường tròn tại M cắt AN ở D.
a) Chứng minh: 4 điểm A, D, M , O cùng thuộc một đường tròn
b) Chứng minh: OD // BM và suy ra D là trung điểm của AN
c) Đường thẳng kẻ qua O và vuông góc với BM cắt tia DM ở E. Chứng minh: BE là tiếp tuyến của đường tròn (O ; R)
d) Qua O kẻ đường thẳng vuông góc với AB và cắt đường thẳng BM tại I. Gọi giao điểm của AI và BD là J. Khi điểm M di động trên (O ; R) thì J chạy trên đường nào?
Bài 5: (0,5 điểm) Cho a > 0. Tìm giá trị nhỏ nhất của P = a2 + 4a + 15 +
Vậy với mọi x thỏa mãn điều kiện x ≥ 0;x ≠ 9 thì |M| <
Gọi thời gian vòi 1 chảy 1 mình đầy bể là x (h)
Thời gian vòi 1 chảy 1 mình đầy bể là y (h)
Trong 1h vòi thứ nhất chảy được 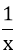
Trong 1h vòi thứ hai chảy được 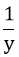
=> Trong 1h cả hai vòi chảy được 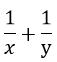
Do cả 2 vòi chảy trong 1 giờ 12 phút thì đầy bể nên ta có phương trình:
Nếu mở vòi thứ nhất chảy trong 30 phút và vòi thứ hai chảy trong 1 giờ thì được 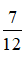
Vậy vòi 1 chảy 1 mình trong 2 giờ thì đầy bể
Vòi 2 chảy 1 mình trong 3 giờ thì đầy bể.
Vậy hệ phương trình có nghiệm (x; y) = (6; 8)
2) Tọa độ giao điểm của 2 đường thẳng là nghiệm của hệ phương trình:
Vậy tọa độ giao điểm của 2 đường thẳng trên là M (2; 3)
Gọi N là giao điểm của đường thẳng y = 2x – 1 với Oy => N (0; -1)
Gọi P là giao điểm của đường thẳng y = 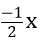
Gọi E là hình chiếu vuông góc của M trên Oy
SPMN = 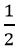
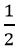
∠DMO =90o (do M là tiếp tuyến của (O))
∠DAO =90o (do AD là tiếp tuyến của (O))
=> Tứ giác ADMO là tứ giác nội tiếp.
b) Do D là giao điểm của 2 tiếp tuyến DM và DA nên OD là tia phân giác của ∠AOM
Mặt khác ta có (ABM là góc nội tiếp chắn cung AM
OM// BM; O là trung điểm của AB
c) Ta có: ΔOBM cân tại O ;OE ⊥MB =>OE là đường trung trực của MB
=>EM = EB => ΔMEB cân tại E => ∠EMB = ∠MEB (1)
ΔOBM cân tại O => ∠OMB = ∠OBM (2)
Cộng (1) và (2) vế với vế, ta được:
∠EMB + ∠OMB = ∠MEB + ∠OBM ⇔ ∠EMO =∠EOB ⇔ ∠EOB =90o
d) Lấy điểm E trên tia OA sao cho OE =
Xét tam giác OAI có OI vừa là đường cao vừa là trung tuyến
=> Tam giác OAI cân tại I => IA = IB; ∠IBA = ∠IAB
=> ∠NAI = ∠INA => ΔINA cân tại I => IA = IN
Tam giác NAB vuông tại A có: IA = IN = IB
=> IA là trung tuyến của tam giác NAB
IA và BD là trung tuyến; IA ∩ BD = {J}
=> J là trọng tâm của tam giác BNA
=> J nằm trên đường thẳng d vuông góc với AB và cách O một khoảng bằng R/3.
Phần đảo: Lấy điểm J’ bất kì thuộc đường thẳng d
Do d// OI (cùng vuông góc AB) nên ta có:
AI là trung tuyến của tam giác NAB
=> J’ là trọng tâm tam giác NAB
Vậy khi M di chuyển trên (O) thì J di chuyển trên đường thẳng d vuông góc với AB và cách O một khoảng là R/3.
tag: 2019 2018 2020 2016 ôn 2017 tuyển tập tỉnh dđề quảng ngãi chuyên hải phòng 2015 sinh giáo tài liệu 2014 chinh phục 2006 2013 lạng sơn pdf thanh hóa violet bình 2016-2017 2003 tổng hợp dđáp ngoại ngữ nguyễn huệ thành phố hồ chí tphcm hưng yên hoà lào cai quận hoàn kiếm 2012 2009 2010 bộ 2011 bái

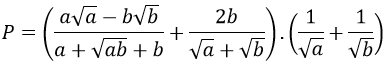
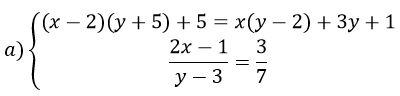
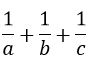 ≥ 6
≥ 6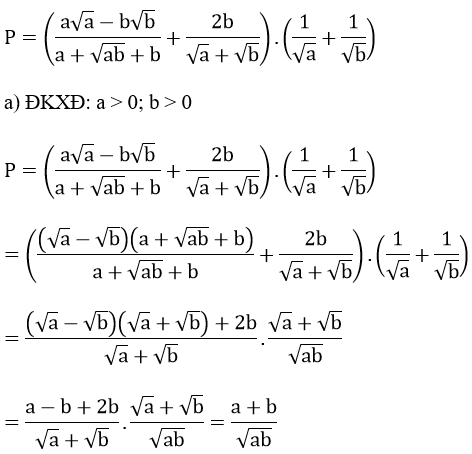
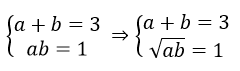
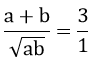 = 3
= 3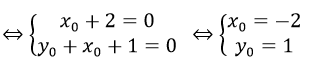
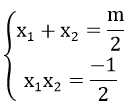
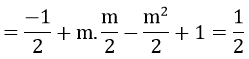
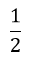
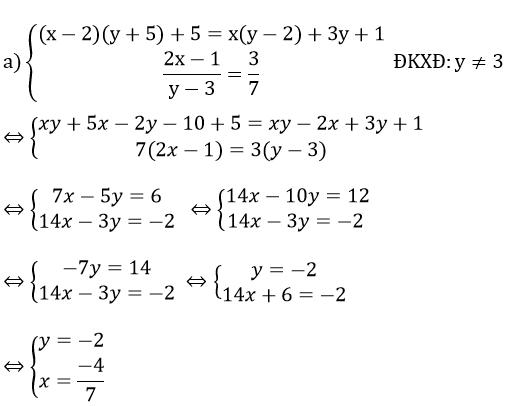
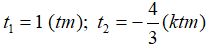
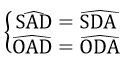 => ∠SAD + ∠OAD = ∠SDA + ∠ODA
=> ∠SAD + ∠OAD = ∠SDA + ∠ODA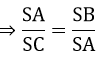 => SB.SC = SA2 (1)
=> SB.SC = SA2 (1)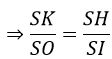 => SK.SI = SH.SO (3)
=> SK.SI = SH.SO (3)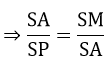 => SP.SM = SA2
=> SP.SM = SA2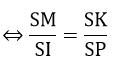
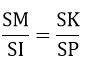
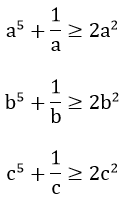
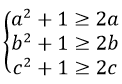
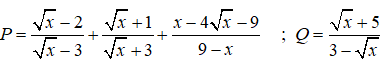
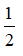
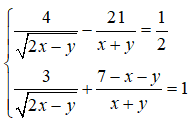
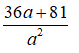
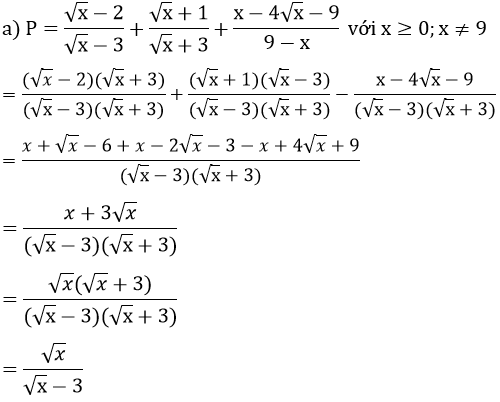
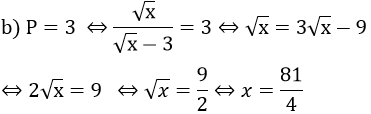
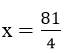 thì P = 3
thì P = 3