Công thức tích phân cơ bản

 Công thức tích phân cơ bản

 Ta có $y=x^3$ là một nguyên hàm của $\frac{dy}{dx}=3x^2$ . Ngoài ra ta còn vô số nguyên hàm khác, chẳng hạn như: $y=x^3+4y=x^3+\pi y=x^3+27.3$ Tổng quát, ta nói $y=x^3+K$ là tích phân bất định (hay nguyên hàm) của $3x^2$ . Con số ? được gọi là hằng số tích phân.

 2. Dấu tích phân

 Ký hiệu ∫ hình thành bởi sự kéo dài ký tự “?” viết tắt của chữ “sum” (tổng) (Người Đức, Anh thời xưa viết chữ “?” giống với ký hiệu tích phân bây giờ). ∑ là ký hiệu của “tổng”. Nó được dùng cho tổng hữu hạn hay vô hạn. ∫ là ký hiệu của tổng hữu hạn các diện tích vô cùng nhỏ (hoặc các biến vô cùng nhỏ khác). Ký hiệu chữ “?” dài này được Lebniz giới thiệu khi ông phát triển một số khái niệm của tích phân.

 3. Tích phân hằng số

 $\int kdx=kx+K$ (? và ? là các hằng số).

 4. Tích phân lũy thừa của ?

 $\int x^{n}dx=\frac{x^{n+1}}{n+1}+K$ Công thức này đúng khi ? ≠ −1. Khi tích phân lũy thừa của ?, ta thêm 1 vào lũy thừa và chia biến lũy thừa mới cho giá trị lũy thừa mới.

 II. Bảng tích phân

 1. Tích phân cơ bản

• $\int 0du=C,\int dx=x+C$
• $\int u^{a}du=\frac{u^{a+1}}{a+1}+C$ với $a\ne -1,a\in R$
• $\int \frac{du}{u}=ln|u|+C$
• $\int e^{u}du=e^u+C$
• $\int cosudu=sinu+C$
• $\int sinudu=-cosu+C$
• $\int \frac{1}{co{s}^{2}u}du=tanu+C$
• $\int \frac{1}{si{n}^{2}u}du=-cotu+C$
• $\int \frac{1}{\sqrt{1-u^2}}du=\{\begin{array}{c}arcsinu+C\\ -arccosu+C\end{array}$
• $\int \frac{1}{\sqrt{1+u^2}}du=\{\begin{array}{c}arctanu+C\\ -arccotu+C\end{array}$

 2. Tích phân từng phần

 Công thức tính tích phân từng phần:

 Theo qui tắc lấy đạo hàm một tích:

 $d\left(uv\right)=udv+vdu$

 Lấy tích phân cả hai vế ta được:

 $uv=\int udv+\int vdu$

 Từ đây ta có công thức sau:

 $\int udv=uv-\int vdu$

 3. Tích phân lượng giác

 Giả sử ta cần tính tích phân

 $I=\int R(sin,cos)dx$

 trong đó R là hàm hữu tỉ của hai đối số. Ta có thể hữu tỉ hoá tích phân trên bằng cách đặt $t=tan\frac{x}{2}$. Thật vậy:

 $sinx=\frac{2t}{1+t^2},cosx=\frac{1-t^2}{1+t^2},x=2arctant,dx=\frac{2dt}{1+t^2}$

 Do đó, có thể đưa ra tích phân I về dạng:

 $I=\int R(\frac{2t}{1+t^2},\frac{1-t^2}{1+t^2}).\frac{2dt}{1+t^2}$

 4. Tích phân xác định

 Cách tính tích phân xác định:

 ${\int }_a^{b}f\left(x\right)dx=F\left(x\right){|}_a^b=F\left(b\right)-F\left(a\right)$

• ?(?) là nguyên hàm của ?(?).
• ?(?) là giá trị nguyên hàm ứng với cận trên ? = ?.
• ?(?) là giá trị nguyên hàm ứng với cận dưới ? = ?.

 Biểu thức này gọi là tích phân xác định.

 5. Tích phân mở rộng

 

 Đặt ẩn phụ trong tích phân xác định:

 Nhắc lại công thức lũy thừa của tích phân: $\int u^{n}du=\frac{u^{n+1}}{n+1}+K,$ (với ? ≠ 1)

 Khi ta dùng ẩn phụ, tức ta đã thay đổi biến nên ta không thể dùng cận trên và cận dưới của biến đó. Ta có thể giải quyết bài toán theo cách của tích phân bất định, sau đó dùng cận trên và cận dưới. Giải bài toán theo biến mới và cận trên, cận dưới mới. Biểu diễn biến cũng như giá trị hai cận ban đầu trong toàn bộ quá trình đặt ẩn phụ.

 Công thức tích phân từng phần

 Trong vi tích phân nói riêng, và trong giải tích toán học nói chung, tích phân từng phần là quá trình tìm tích phân của tích các hàm dựa trên tích phân các đạo hàm và nguyên hàm của chúng. Nó thường được sử dụng để biến đổi nguyên hàm của tích các hàm thành một nguyên hàm mà đáp án có thể được tìm thấy dễ dàng hơn. Quy tắc có thể suy ra bằng cách tích hợp quy tắc nhân của đạo hàm.

 Nếu u = u(x) và du = u′(x) dx, trong đó v = v(x) và dv = v′(x) dx, thì tích phân từng phần phát biểu rằng:

{\displaystyle {\displaystyle {\begin{aligned}\int _{a}^{b}u(x)v'(x)\,dx&=[u(x)v(x)]_{a}^{b}-\int _{a}^{b}u'(x)v(x)dx\\&=u(b)v(b)-u(a)v(a)-\int _{a}^{b}u'(x)v(x)\,dx\end{aligned}}}}

 hay gọn hơn:

{\displaystyle \int u\,dv=uv-\int v\,du.\!}

 Có các công thức tổng quát hơn của tích phân từng phần cho tích phân Riemann-Stieltjes và tích phân Lebesgue-Stieltjes. Chuỗi số cũng có mô hình rời rạc tương tự gọi là tổng từng phần.

Tích của hai hàm[sửa | sửa mã nguồn]

 Định lý có thể được suy ra như sau. Giả sử u(x) và v(x) là hai hàm khả vi liên tục. Quy tắc nhân phát biểu rằng (theo ký hiệu của Leibniz):

{\displaystyle {\frac {d}{dx}}{\Big (}u(x)v(x){\Big )}=v(x){\frac {d}{dx}}\left(u(x)\right)+u(x){\frac {d}{dx}}\left(v(x)\right).\!}

 Tích phân cả hai vế đối với x,

{\displaystyle \int {\frac {d}{dx}}\left(u(x)v(x)\right)\,dx=\int u'(x)v(x)\,dx+\int u(x)v'(x)\,dx}

 sau đó áp dụng định nghĩa của nguyên hàm,

{\displaystyle u(x)v(x)=\int u'(x)v(x)\,dx+\int u(x)v'(x)\,dx}

{\displaystyle \int u(x)v'(x)\,dx=u(x)v(x)-\int u'(x)v(x)\,dx}

 cho ta công thức tích phân từng phần.

 Bởi vì du và dv là các vi phân của một hàm một biến x,

{\displaystyle du=u'(x)dx\quad dv=v'(x)dx}

{\displaystyle \int u(x)\,dv=u(x)v(x)-\int v(x)\,du}

 Tích phân gốc ∫uv′ dx chứa v′ (đạo hàm của v); để áp dụng định lý, phải tim nguyên hàm v (của v′), và tính tích phân ∫vu′ dx.

Mở rộng cho các trường hợp khác[sửa | sửa mã nguồn]

 Điều kiện u và v khả vi liên tục là không thực cần thiết. Tích phân từng phần chỉ được áp dụng nếu u là liên tục tuyệt đối và hàm được chọn v’ phải khả tích Lebesgue (nhưng không nhất thiết là liên tục).^[1] (Nếu v’ có một điểm gián đoạn thì nguyên hàm v của nó có thể không có đạo hàm tại điểm đó.)

 Nếu khoảng tích phân không phải là không gian compact thì u không cần thiết phải hoàn toàn liên tục trong toàn khoảng hoặc v ‘ không cần thiết phải là khả tích Lebesgue trong khoảng, như một vài ví dụ sẽ cho thấy, trong đó u và v là liên tục và khả vi liên tục. Ví dụ nếu

{\displaystyle u(x)=\exp(x)/x^{2},\,v'(x)=\exp(-x)}

 u không liên tục hoàn toàn trên khoảng [1, +∞), tuy nhiên

{\displaystyle \int _{1}^{\infty }u(x)v'(x)\,dx=\left[u(x)v(x)\right]_{1}^{\infty }-\int _{1}^{\infty }u'(x)v(x)\,dx}

 miễn là {\displaystyle \left[u(x)v(x)\right]_{1}^{\infty }} có nghĩa là giới hạn {\displaystyle u(L)v(L)-u(1)v(1)} khi{\displaystyle L\to \infty } và miễn là hai số hạng ở vế phải hữu hạn. Điều này chỉ đúng khi chúng ta chọn {\displaystyle v(x)=-\exp(-x).} Tương tự, nếu

{\displaystyle u(x)=\exp(-x),\,v'(x)=x^{-1}\sin(x)}

 v’ không khả vi Lebesgue trên khoảng [1, +∞), tuy nhiên

{\displaystyle \int _{1}^{\infty }u(x)v'(x)\,dx=\left[u(x)v(x)\right]_{1}^{\infty }-\int _{1}^{\infty }u'(x)v(x)\,dx}

 với giải thích tương tự.

 Người ta cũng có thể dễ dàng đưa ra những ví dụ như thế này nhưng trong đó u và v không khả vi liên tục.

Tích của nhiều hàm[sửa | sửa mã nguồn]

 Áp dụng quy tắc tích để tìm tích phần cho ba hàm nhân nhau, u(x), v(x), w(x), cho kết quả tương tự:

{\displaystyle \int _{a}^{b}uv\,dw=[uvw]_{a}^{b}-\int _{a}^{b}uw\,dv-\int _{a}^{b}vw\,du.}

 Tổng quát với n thừa số

{\displaystyle {\frac {d}{dx}}\left(\prod _{i=1}^{n}u_{i}(x)\right)=\sum _{j=1}^{n}\prod _{i\neq j}^{n}u_{i}(x){\frac {du_{j}(x)}{dx}},}

 dẫn đến

{\displaystyle {\Bigl [}\prod _{i=1}^{n}u_{i}(x){\Bigr ]}_{a}^{b}=\sum _{j=1}^{n}\int _{a}^{b}\prod _{i\neq j}^{n}u_{i}(x)\,du_{j}(x),}

 trong đó tích thuộc tất cả các hàm ngoại trừ một hàm được lấy đạo hàm trong cùng số hạng.

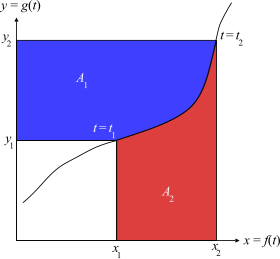
Sự hình dung[sửa | sửa mã nguồn]

 Xem xét đường cong tham số bởi (x, y) = (f(t), g(t)). Giả sử rằng đường cong là đơn ánh cục bộ và khả tích cục bộ, ta định nghĩa

{\displaystyle x(y)=f(g^{-1}(y))}

{\displaystyle y(x)=g(f^{-1}(x))}

 Diện tích vùng màu xanh là

{\displaystyle A_{1}=\int _{y_{1}}^{y_{2}}x(y)dy}

 Tương tự như vậy, diện tích của vùng màu đỏ là

{\displaystyle A_{2}=\int _{x_{1}}^{x_{2}}y(x)dx}

 Tổng diện tích A₁ + A₂ bằng diện tích của hình chữ nhật lớn hơn, x₂y₂, trừ đi diện tích của hình chữ nhật nhỏ hơn, x₁y₁:

{\displaystyle \overbrace {\int _{y_{1}}^{y_{2}}x(y)dy} ^{A_{1}}+\overbrace {\int _{x_{1}}^{x_{2}}y(x)dx} ^{A_{2}}={\biggl .}x.y(x){\biggl |}_{x1}^{x2}={\biggl .}y.x(y){\biggl |}_{y1}^{y2}}

 Hoặc theo tham số t

 {\displaystyle {\displaystyle \int _{t_{1}}^{t_{2}}x(t)dy(t)+\int _{t_{1}}^{t_{2}}y(t)dx(t)={\biggl .}x(t)y(t){\biggl |}_{t_{1}}^{t_{2}}}}

 Hoặc biễu diễn theo nguyên hàm:

{\displaystyle \int xdy+\int ydx=xy}

 Chỉnh lại:

{\displaystyle \int xdy=xy-\int ydx}

 Từ đó tích phân từng phần có thể coi là diện tích của vùng màu xanh trong tổng diện tích và diện tích của vùng đỏ.

 Sự hình dung này cũng lý giải việc tích phân từng phần có thể tính tích phân của hàm nghịch đảo f⁻¹(x) khi đã biết tích phân của f(x). Thật vậy, nếu hàm x(y) và y(x) là nghịch đảo của nhau thì có thể tìm tích phân ∫x dy khi đã biết tích phân ∫y dx. Cụ thể, điều này giải thích việc kết hợp sử dụng tích phân từng phần với hàm logarithm và hàm lượng giác nghịch đảo.

Ứng dụng để tìm nguyên hàm[sửa | sửa mã nguồn]

Kịch bản[sửa | sửa mã nguồn]

 Tích phân từng phần là một quá trình suy nghiệm hơn là một quá trình máy móc thuần tuý để tính toán tích phân; cho một hàm đơn để tích phân, các chiến lược điển hình là cẩn thận tách nó thành tích của hai hàm u(x)v(x) sao cho tích phân được tạo bởi công thức tích phân từng phần dễ tính toán hơn so với tích phân gốc. Công thức sau minh họa kịch bản trường hợp tốt nhất:

{\displaystyle \int uv\ dx=u\int v\ dx-\int \left(u’\int v\ dx\right)\ dx.}

 Lưu ý rằng ở vế phải, u được lấy đạo hàm và v được lấy tích phân; do đó sẽ hữu ích khi chọn u là một hàm có thể giản hóa khi lấy đạo hàm, hoặc khi chọn v là hàm đơn giản hóa được khi được lấy tích phân. Xét ví dụ đơn giản sau:

{\displaystyle {\displaystyle \int {\frac {\ln(x)}{x^{2}}}\ dx\ .}}

 Do đạo hàm của ln(x) là 1/x, ta chọn (ln(x)) là u; do nguyên hàm của1/x² là –1/x, chọn 1/x²dx làm dv. Từ đó ta có:

{\displaystyle {\displaystyle \int {\frac {\ln(x)}{x^{2}}}\ dx=-{\frac {\ln(x)}{x}}-\int {\biggl (}{\frac {1}{x}}{\biggr )}{\biggl (}-{\frac {1}{x}}{\biggr )}\ dx\ .}}

 Nguyên hàm của {\displaystyle -{\frac {1}{x^{2}}}} có thể được tìm thấy bằng quy tắc luỹ thừa và bằng {\displaystyle {\frac {1}{x}}}.

 Ngoài ra, người ta có thể chọn u và v sao cho tích u’ (∫v dx) triệt tiêu nhau. Ví dụ, giả sử ta muốn tích phân:

{\displaystyle \int \sec ^{2}(x)\cdot \ln {\Big (}{\bigl |}\sin(x){\bigr |}{\Big )}\ dx.}

 Nếu chúng ta chọn u(x) = ln(|sin(x)|) và v(x) = sec²x, thì u được lấy vi phân tới 1/ tan x bằng cách sử dụng quy tắc chuỗi và v được lấy tích phân tan x; do đó công thức cho:

{\displaystyle {\displaystyle \int \sec ^{2}(x)\cdot \ln {\Big (}{\bigl |}\sin(x){\bigr |}{\Big )}\ dx=\tan(x)\cdot \ln {\Big (}{\bigl |}\sin(x){\bigr |}{\Big )}-\int \tan(x)\cdot {\frac {1}{\tan(x)}}dx\ .}{\displaystyle \int \sec ^{2}(x)\cdot \ln {\Big (}{\bigl |}\sin(x){\bigr |}{\Big )}\ dx=\tan(x)\cdot \ln {\Big (}{\bigl |}\sin(x){\bigr |}{\Big )}-\int \tan(x)\cdot {\frac {1}{\tan(x)}}dx\ .}}

 Hàm lấy tích phân trở thành 1 và có nguyên hàm là x. Tìm ra sự kết hợp co thể giản hóa thường cần thử sai.

 Trong một số trường hợp, không đảm bảo rằng tích phân tạo bởi tích phân từng phần sẽ có dạng đơn giản; Ví dụ, trong giải tích số, ta có thể chấp nhận khi chỉ tạo ra một số sai sót nhỏ. Một số kỹ thuật đặc biệt khác được chứng minh trong các ví dụ dưới đây.

Hàm đa thức và hàm lượng giác

 Để tính

{\displaystyle I=\int x\cos(x)\ dx\,}

 đặt:

{\displaystyle u=x\ \Rightarrow \ du=dx}

{\displaystyle dv=\cos(x)\ dx\ \Rightarrow \ v=\int \cos(x)\ dx=\sin(x)}

 thì:

{\displaystyle {\begin{aligned}\int x\cos(x)\ dx&=\int u\ dv\\&=u\cdot v-\int v\,du\\&=x\sin(x)-\int \sin(x)\ dx\\&=x\sin(x)+\cos(x)+C,\end{aligned}}\!}

 với C là hằng số tích phân.

 Đối với bậc cao hơn của x trong dạng

{\displaystyle \int x^{n}e^{x}\ dx,\ \int x^{n}\sin(x)\ dx,\ \int x^{n}\cos(x)\ dx\,}

 sử dụng nhiều lần tích phân từng phần có thể tính các tích phân thuộc loại này; mỗi lần sử dụng sẽ giảm một bậc của x.

Hàm mũ và hàm lượng giác

 Một ví dụ thường dùng để tính tích phân từng phần là

{\displaystyle I=\int e^{x}\cos(x)\ dx.}

 Ở đây, ta thực hiện tích phân từng phần hai lần. Đầu tiên đặt

{\displaystyle u=\cos(x)\ \Rightarrow \ du=-\sin(x)\ dx}

{\displaystyle dv=e^{x}\ dx\ \Rightarrow \ v=\int e^{x}\ dx=e^{x}}

 thì:

{\displaystyle \int e^{x}\cos(x)\ dx=e^{x}\cos(x)+\int e^{x}\sin(x)\ dx.}

 Giờ, để tính tích phân còn lại, chúng ta sử dụng tích phân từng phần một lần nữa, với:

{\displaystyle u=\sin(x)\ \Rightarrow \ du=\cos(x)\ dx}

{\displaystyle dv=e^{x}\ dx\ \Rightarrow \ v=\int e^{x}\ dx=e^{x}.}

 thì:

{\displaystyle \int e^{x}\sin(x)\ dx=e^{x}\sin(x)-\int e^{x}\cos(x)\ dx.}

 Kết hợp lại,

{\displaystyle \int e^{x}\cos(x)\ dx=e^{x}\cos(x)+e^{x}\sin(x)-\int e^{x}\cos(x)\ dx.}

 Tích phân giống nhau xuất hiện trên cả hai vế của phương trình này. Thêm tích phân cần tính vào 2 vế, ta có

{\displaystyle 2\int e^{x}\cos(x)\ dx=e^{x}{\bigl (}\sin(x)+\cos(x){\bigr )}+C}

 mà trở thành:

{\displaystyle \int e^{x}\cos(x)\ dx={\frac {e^{x}{\bigl (}\sin(x)+\cos(x){\bigr )}}{2}}+C’}

 trong đó C (và C‘ = C/2) là các hằng số tích phân.

 Phương pháp tương tự được sử dụng để tìm tích phân của hàm sec bậc ba.

Các hàm được nhân với phần tử đơn vị

 Hai ví dụ nổi tiếng khác khi áp dụng tích phân từng phần cho một hàm được biểu diễn là tích của 1 và chính nó. Có thể tính tích phân này nếu biết đạo hàm của hàm đó và tích phân của đạo hàm này nhân x.

 Ví dụ đầu tiên là ∫ ln(x) dx. Chúng ta viết tích phân này như:

{\displaystyle {\displaystyle I=\int \ln(x)\cdot 1\ dx\ .}}

 Đặt:

{\displaystyle u=\ln(x)\ \Rightarrow \ du={\frac {dx}{x}}}

{\displaystyle dv=dx\ \Rightarrow \ v=x}

 thì:

{\displaystyle {\begin{aligned}\int \ln(x)\ dx&=x\ln(x)-\int {\frac {x}{x}}\ dx\\&=x\ln(x)-\int 1\ dx\\&=x\ln(x)-x+C\end{aligned}}}

 trong đó C là hằng số tích phân.

 Ví dụ thứ hai là hàm tan nghịch arctan(x):

{\displaystyle I=\int \arctan(x)\ dx.}

 Viết lại

{\displaystyle \int \arctan(x)\cdot 1\ dx.}

 Đặt:

{\displaystyle u=\arctan(x)\ \Rightarrow \ du={\frac {dx}{1+x^{2}}}}

{\displaystyle dv=dx\ \Rightarrow \ v=x}

 thì

{\displaystyle {\begin{aligned}\int \arctan(x)\ dx&=x\cdot \arctan(x)-\int {\frac {x}{1+x^{2}}}\ dx\\[8pt]&=x\cdot \arctan(x)-{\frac {\ln(1+x^{2})}{2}}+C\end{aligned}}}