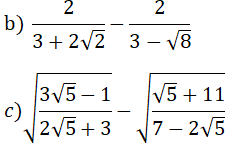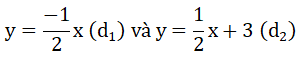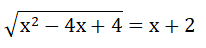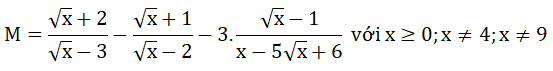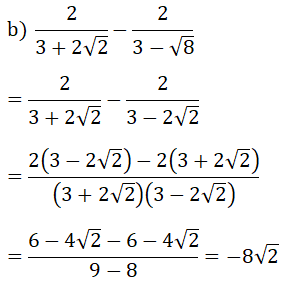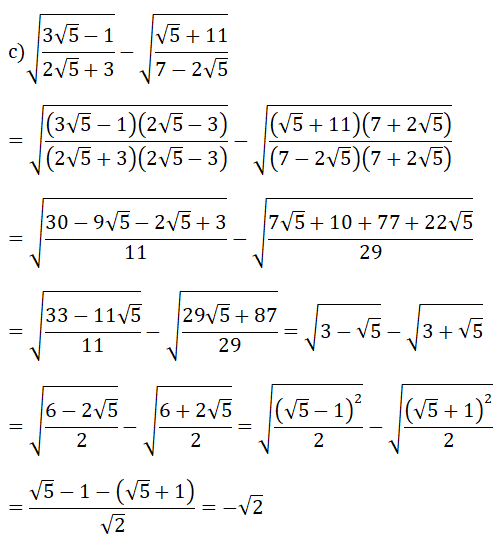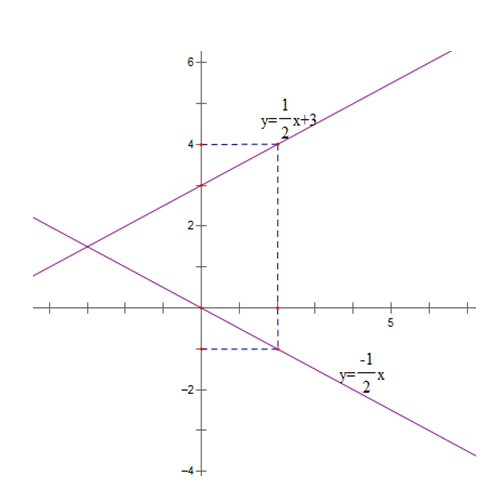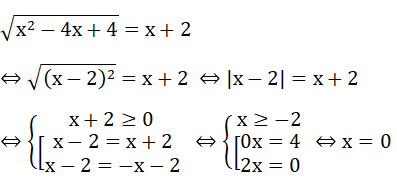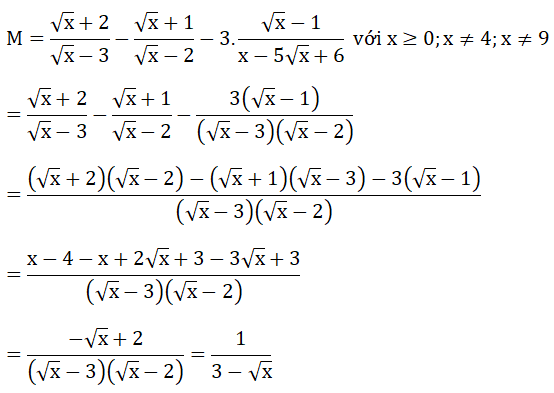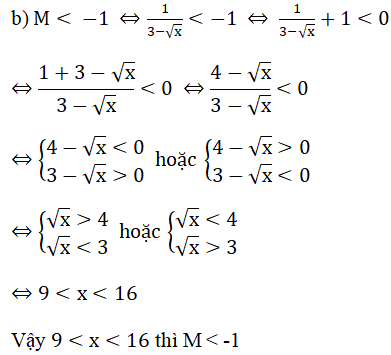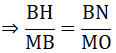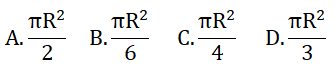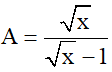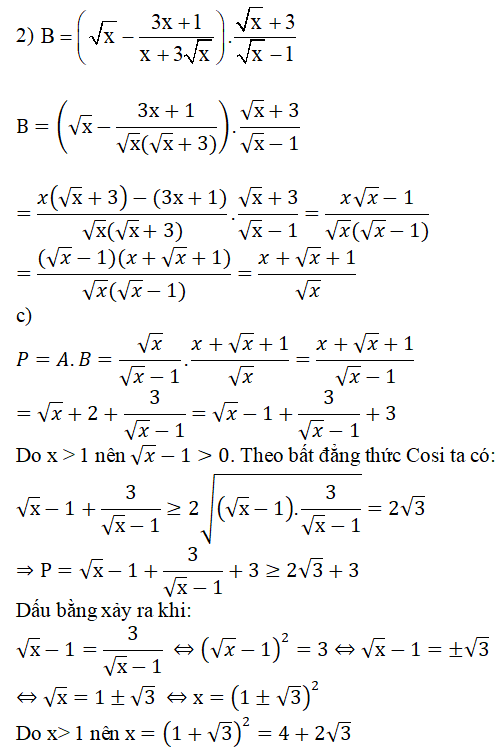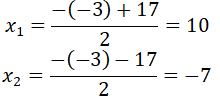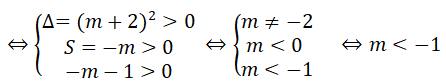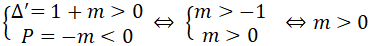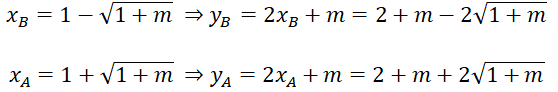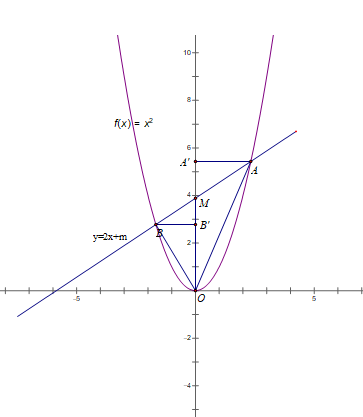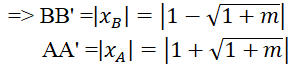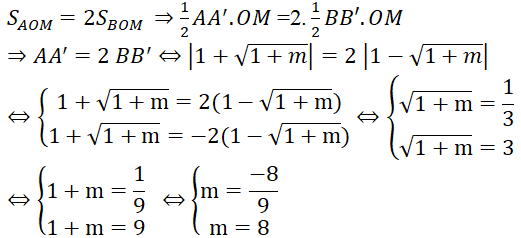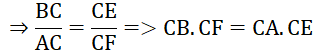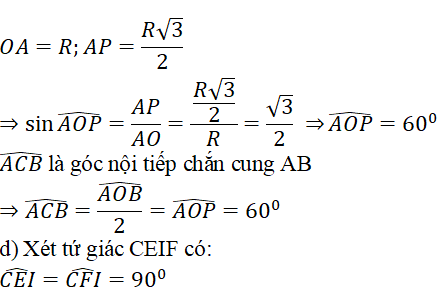Đề thi toán 9

 Đề thi học kì 1 toán 9

 Đề thi Học kì 1 Toán lớp 9 có đáp án (Đề 1)

 Thời gian làm bài: 90 phút

 Đề bài

 Bài 1: (1.5 điểm) Thực hiện các phép tính:

 a) 4√24 – 3√54 + 5√6 – √150

 Bài 2: (1.5 điểm) Vẽ trên cùng một mặt phẳng tọa độ Oxy đồ thị của các hàm số sau:

 Xác định b để đường thẳng (d₃ ) y = 2x + b cắt (d₂ ) tại điểm có hoành độ và tung độ đối nhau.

 Bài 3: (1.5 điểm) Giải phương trình:

 Bài 4: (2 điểm) Cho biểu thức:

 a) Thu gọn biểu thức M.

 b) Tìm giá trị của x để M < – 1 .

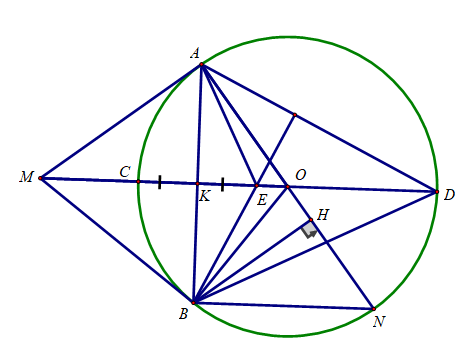
 Bài 5: (3.5 điểm) Cho đường tròn (O;R) và điểm M ở ngoài đường tròn sao cho OM=8/5 R . Kẻ các tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm), đường thẳng AB cắt OM tại K.

 a) Chứng minh K là trung điểm của AB.

 b) Tính MA, AB, OK theo R.

 c) Kẻ đường kính AN của đường tròn (O). Kẻ BH vuông góc với AN tại H. Chứng minh MB.BN = BH.MO .

 d) Đường thẳng MO cắt đường tròn (O) tại C và D (C nằm giữa O và M). Gọi E là điểm đối xứng của C qua K. Chứng minh E là trực tâm của tam giác ABD.

 Đáp án và Hướng dẫn giải

 Bài 1: (1.5 điểm)

 a) 4√24 – 3√54 + 5√6 – √150

 = 8√6 – 9√6 + 5√6 – 5√6

 = -√6

 Bài 2: (1.5 điểm)

 a) Tập xác định của hàm số R

 Bảng giá trị

 b) Gọi A (m; – m) là tọa độ giao điểm của (d₂ ) và (d₃)

 Khi đó:

 -m = 1/2 m + 3 ⇔ 3/2 m = 3 ⇔ m = 2

 Vậy tọa độ giao điểm của d₂ và d₃ là (2; -2)

 ⇒ -2 = 2.2 + b ⇔ b = -6

 Vậy b = – 6

 Bài 3: (1.5 điểm)

 Vậy phương trình có nghiệm x = 0

 Bài 4: (2 điểm)

 a) Rút gọn M

 Bài 5: (3.5 điểm)

 a) Ta có:

 MA = MB ( tính chất 2 tiếp tuyến cắt nhau)

 OA = OB ( cùng bằng bán kính đường tròn (O)

 ⇒ OM là đường trung trực của AB

 OM ∩ AB = K ⇒ K là trung điểm của AB

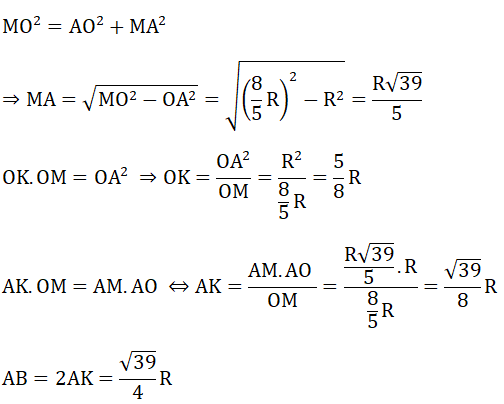
 b) Tam giác MAO vuông tại A, AK là đường cao có:

 c) Ta có: ∠(ABN ) = 90^o(B thuộc đường tròn đường kính AN)

 ⇒ BN // MO ( cùng vuông góc với AB)

 Do đó:

 ∠(AOM) = ∠(ANB) (đồng vị))

 ∠(AOM) = ∠(BOM) (OM là phân giác ∠(AOB))

 ⇒ ∠(ANB) = ∠(BOM)

 Xét ΔBHN và ΔMBO có:

 ∠(BHN) = ∠(MBO ) = 90^o

 ∠(ANB) = ∠(BOM)

 ⇒ ΔBHN ∼ ΔMBO (g.g)

 Hay MB. BN = BH. MO

 d) Ta có:

 K là trung điểm của CE (E đối xứng với C qua AB)

 K là trung điểm của AB

 AB ⊥ CE (MO ⊥ AB)

 ⇒ Tứ giác AEBC là hình thoi

 ⇒ BE // AC

 Mà AC ⊥ AD (A thuộc đường tròn đường kính CD)

 Nên BE ⊥ AD và DK ⊥ AB

 Vậy E là trực tâm của tam giác ADB

 Đề thi hk2 toán 9

Đề thi Toán lớp 9 Học kì 2 (Đề số 1)

 Thời gian làm bài: 90 phút

 Đề bài

Phần trắc nghiệm (2 điểm)

 Câu 1: Cho hàm số y = -3x². Kết luận nào sau đây là đúng :

 A. Hàm số trên luôn đồng biến

 B. Hàm số trên luôn nghịch biến

 C. Hàm số trên đồng biến khi x > 0, nghịch biến khi x < 0

 D. Hàm số trên đồng biến khi x < 0, nghịch biến khi x > 0

 Câu 2: Cho phương trình bậc hai x² – 2(m + 1) x + 4m = 0. Phương trình có nghiệm kép khi m bằng:

 A. 1       C. Với mọi m

 B. –1       D. Một kết quả khác

 Câu 3: Cung AB của đường tròn (O; R) có số đo là 60^o. Khi đó diện tích hình quạt AOB là:

 Câu 4: Tứ giác MNPQ nội tiếp đường tròn khi:

 A.∠(MNP) + ∠(NPQ) = 180^o

 B.∠(MNP) = ∠(MPQ)

 C. MNPQ là hình thang cân

 D. MNPQ là hình thoi

Phần tự luận (8 điểm)

 Bài 1 (2,0 điểm)

 1) Tìm điều kiện xác định của biểu thức 

 2) Cho biểu thức 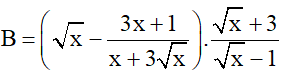 với x > 0; x ≠ 1

 a) Rút gọn biểu thức B

 b) Tìm giá trị nhỏ nhất của P = A.B với x > 1

 Bài 2 (1,5 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình

 Một tấm bìa hình chữ nhật có chiều dài hơn chiều rộng 3dm. Nếu giảm chiều rộng đi 1dm và tăng chiều dài thêm 1dm thì diện tích tấm bìa là 66 Tính chiều rộng và chiều dài của tấm bìa lúc ban đầu.

 Bài 3 (2,0 điểm)

 1) Cho phương trình x⁴ + mx² – m – 1 = 0(m là tham số)

 a) Giải phương trình khi m = 2

 b) Tìm giá trị của m để phương trình có 4 nghiệm phân biệt.

 2) Trong mặt phẳng tọa độ Oxy cho parabol (P): y = x² và đường thẳng (d): y = 2x + m (m là tham số).

 a) Xác định m để đường thẳng (d) tiếp xúc với parabol (P). Tìm hoành độ tiếp điểm.

 b) Tìm giá trị của m để đường thẳng (d) cắt parabol (P) tại hai điểm A, B nằm về hai phía của trục tung, sao cho diện tích có diện tích gấp hai lần diện tích (M là giao điểm của đường thẳng d với trục tung).

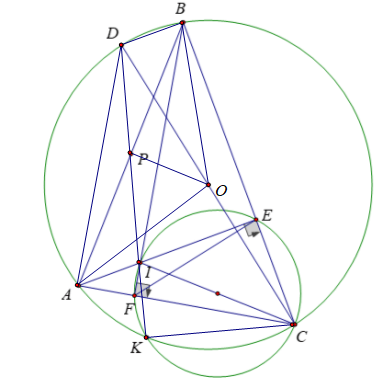
 Bài 4 (3,5 điểm) Cho đường tròn (O; R), dây AB. Trên cung lớn AB lấy điểm C sao cho A < CB. Các đường cao AE và BF của tam giác ABC cắt nhau tại I.

 a) Chứng minh tứ giác AFEB là tứ giác nội tiếp

 b) Chứng minh CF.CB = CE.CA

 c) Nếu dây AB có độ dài bằng R√3 , hãy tính số đo của (ACB)

 d) Đường tròn ngoại tiếp tam giác CEF cắt đường tròn (O; R) tại điểm thứ hai là K (K khác C). Vẽ đường kính CD của (O; R). Gọi P là trung điểm của AB. Chứng minh rằng ba điểm K, P, D thẳng hàng.

 Hướng dẫn giải

Phần trắc nghiệm (2 điểm)

Phần tự luận (8 điểm)

 Bài 1

 Biểu thức A xác định khi √x – 1 ≠ 0 ⇔ √x ≠ 1 ⇔ x ≠ 1

 Vậy GTNN của P là 2√3 + 3 đạt được khi x = 4 + 2√3

 Bài 2

 Gọi chiều dài của tấm bìa là x (x > 3) (dm)

 ⇒ Chiều rộng của tấm bìa là x – 3 (dm)

 Nếu tăng chiều dài 1 dm và giảm chiều rộng 1 dm thì diện tích là 66 dm² nên ta có phương trình:

 (x + 1)(x – 3 – 1) = 66

 ⇔ (x + 1)(x – 4 ) = 66

 ⇔ x² – 3x – 4 – 66 = 0

 ⇔ x² – 3x – 70 = 0

 Δ = 3² – 4.(-70) = 289 ⇒ √Δ = 17

 ⇒ Phương trình đã cho có 2 nghiệm

 Do x > 3 nên x =10

 Vậy chiều dài của tấm bìa là 10 dm

 Chiều rộng của tấm bìa là 7 dm.

 Bài 3

 1) x⁴ + mx² – m – 1 = 0

 a) Khi m = 2, phương trình trở thành: x⁴ + 2x² – 3 = 0

 Đặt x² = t (t ≥ 0). Khi đó ta có phương trình: t² + 2t – 3 = 0

 ⇒ Phương trình có nghiệm t = 1 và t = -3 (do phương trình có dạng a + b + c = 0)

 Do t ≥ 0 nên t = 1 ⇒ x² = 1 ⇒ x = ±1

 b) Đặt x² = t (t ≥ 0). Khi đó ta có phương trình: t² – mt – m – 1 = 0 (*)

 Δ = m² – 4(-m – 1) = m² + 4m + 4 = (m + 2)²

 Phương trình đã cho có 4 nghiệm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm dương phân biệt

 2) parabol (P): y = x² ; đường thẳng (d): y = 2x + m (m là tham số).

 a) phương trình hoành độ giao điểm của (P) và (d) là:

 x² = 2x + m ⇔ x² – 2x – m = 0

 Δ’= 1 + m

 (d) tiếp xúc với (P) khi phương trình hoành độ giao điểm có duy nhất 1 nghiệm

 ⇔ Δ’= 1 + m = 0 ⇔ m = -1

 Khi đó hoành độ giao điểm là x = 1

 b) (d) cắt (P) tại 2 điểm A, B phân biệt nằm về 2 phía của trục tung khi và chỉ khi

 Khi đó 2 nghiệm của phương trình là:

 Kẻ BB’ ⊥ OM ; AA’ ⊥ OM

 Ta có:

 S_AOM = 1/2 AA’.OM ; S_BOM = 1/2 BB’.OM

 Theo bài ra:

 Do m > 0 nên m = 8

 Vậy với m = 8 thì thỏa mãn điều kiện đề bài.

 Bài 4

 a) Xét tứ giác AEFB có:

 ∠(AFB) = 90^o ( AF là đường cao)

 ∠(AEB) = 90^o ( BE là đường cao)

 ⇒ 2 đỉnh E và F cùng nhìn cạnh AB dưới 1 góc bằng nhau

 ⇒ AEFB là tứ giác nội tiếp.

 b) Xét ΔBEC và ΔAFC có:

 ∠(BCA) là góc chung

 ∠(BEC) = ∠(AFC) = 90 ^o

 ⇒ ΔBEC ∼ ΔAFC

 c) Gọi P là trung điểm của AB

 Do tam giác OAB cân tại O nên OP ⊥ AB

 Tam giác OAP vuông tại P có:

 ⇒ Tứ giác CEIF là tứ giác nội tiếp và CI là đường kính đường tròn ngoại tiếp tứ giác CEIF

 Ta có: IK ⊥ KC ( góc nội tiếp chắn nửa đường tròn ngoại tiếp tứ giác CEIF)

 DK ⊥ KC (góc nội tiếp chắn nửa đường tròn (O)

 ⇒ D; I; K thẳng hàng (1)

 Ta có:

 DB ⊥ BC (góc nội tiếp chắn nửa đường tròn (O)

 AI ⊥ BC ( AI là đường cao của tam giác ABC)

 ⇒ AI // BD

 DA ⊥ BA(góc nội tiếp chắn nửa đường tròn (O)

 BI ⊥ BA ( BI là đường cao của tam giác ABC)

 ⇒ AD // BI

 Xét tứ giác ADBI có: AI // BD và AD // BI

 ⇒ ADBI là hình bình hành

 Do P là trung điểm của AB ⇒ P là trung điểm của DI

 Hay D; P; I thẳng hàng (2)

 Từ (1) và (2) ⇒ D; P; K thẳng hàng.

 Đề thi hsg toán 9