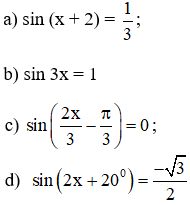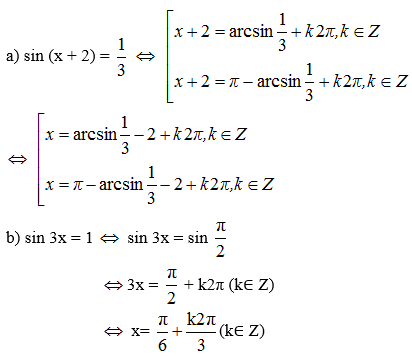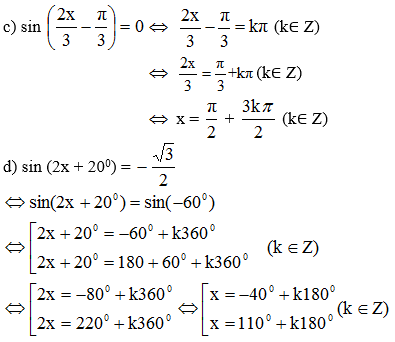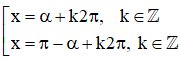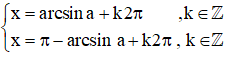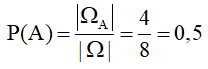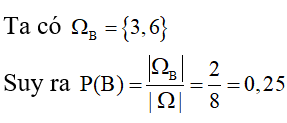Trả lời câu hỏi Toán 11 Đại số Bài 1 trang 4:
a) Sử dụng máy tính bỏ túi, hãy tính sinx, cosx với x là các số sau:
π/6; π/4; 1,5; 2; 3,1; 4,25; 5.
b) Trên đường tròn lượng giác, với điểm gốc A, hãy xác định các điểm M mà số đo của cung AM bằng x (rad) tương ứng đã cho ở trên và xác định sinx, cosx (lấy π ≈ 3,14)
a) sin π/6 = 1/2; cos π/6 = √3/2
sin π/4 = √2/2; cos π/4 = √2/2
sin 1,5 = 0,9975; cos 1,5 = 0,0707
sin 2 = 0,9093; cos 2 = -0,4161
sin 3,1 = 0,0416; cos 3,1 = -0,9991
sin 4,25 = -0,8950; cos 4,25 = -0,4461
sin 5 = -0,9589; cos 5 = 0,2837
a)-1/2 = cos 2π/3 nên cos x = (-1)/2 ⇔ cos x = cos 2π/3
b)cos x = 2/3 ⇒ x = ± arccos 2/3 + k2π, k ∈ Z
c)√3/2 = cos30o nên cos(x + 30o )= √3/2
⇔ x + 30o = ±30o + k360o, k ∈ Z
⇔ x = k360o, k ∈ Z và x = -60o + k360o, k ∈ Z
Bài 1 (trang 28 SGK Đại số 11): Giải các phương trình sau:
+ Phương trình sin x = sin α có các nghiệm
+ Số thực α thỏa mãn 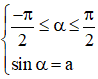
Khi đó phương trình sin x = a có nghiệm
Chọn ngẫu nhiên một số nguyên dương nhỏ hơn 9. Tính xác suất để:
a) Số được chọn là số nguyên tố?
b) Số được chọn chia hết cho 3?
Không gian mẫu Ω = {1, 2, 3, 4, 5, 6, 7, 8}
a) A là biến cố “số được chọn là số nguyên tố”. Ta có ΩA = {2, 3, 5, 7}
Xác suất để số được chọn là số nguyên tố là:
b) Gọi B là biến cố “số được chọn chia hết cho 3”
b) Gọi A là biến cố “Tổng số chấm trên mặt xuất hiện của hai con súc sắc nhỏ hơn hoặc bằng 7”. Liệt kê các kết quả thuận lợi cho A. Tính P(A).
c) Cũng hỏi như trên cho biến cố B: “Có ít nhất một con súc sắc xuất hiện mặt 6 chấm” và C: “Có đúng một con súc sức xuất hiện mặt 6 chấm”
a) Ω = {(a, b)|a, b ∈ N*, 1 ≤ a ≤ 6,1 ≤ b ≤ 6}
b) ΩA = {(6; 1),(5; 1); (5; 2),(4;2),(4;3),(3;1),(3;2),(3;3),(3;4),(2;1),(2;2),(2;3),(2;4),(2;5),(1;1),(1;2),(1;3),(1;4),(1;5),(1;6) }
Tập ΩA có 21 phần tử. Vậy P(A) = 21/36 = 7/12
c) ΩB = {(6;1),(6;2),(6;3),(6;4),(6;5),(6;6),(1;6),(2;6),(3;6),(4;6),(5;6)}
Tập ΩB có 11 phần tử. Vậy P(B) = 11/36
ΩC = {(6;1),(6;2),(6;3),(6;4),(6;5),(1;6),(2;6),(3;6),(4;6),(5;6)}
Tập ΩC có 10 phần tử. Vậy P(C) = 10/36 = 5/18
tag: lớp bt hình học phân phối chương tốt sách giáo khoa trắc nghiệm tổng hợp 37 khoảng cách 29 quy tắc đếm hàm violet đáp án 17 8 18 đạo lim kì giới hạn dãy giai tóm tắt lý thuyết môn trần sĩ tùng nguyễn phú khánh pdf hướng dẫn ôn tổ lê văn đoàn trực tuyến miễn phí quỹ tích tìm cấp cộng online (đủ dạng cả năm hay) hay bắc trung nam 57 97 hệ thống bồi dưỡng sinh giỏi trọng 58 loigiaihay sáng kinh pháp nạp sơ đồ tư duy 54 trong 168 162 casio bổ trợ 92 hiệu 82 chương lớp sách tham khảo giới hạn 121 cách học giỏi giáo án trần sĩ tùng 63 khoa sbt trắc nghiệm kì đáp hình dạng 17 pháp viên pdf ôn thống file word môn hay lim bấm 74 online 169 phép hiệu thẳng vuông góc 132 hinh hoc tổng hợp lý thuyết 58 41 khoảng tài liệu 37 64 54 violet 97 300 đạo hàm làm trọng bồi dưỡng sinh về dãy coông mỹ trong 18 dạy thêm mạng cấp nhân loigiaihay ppct 92 casio fx 570vn plus vietjack tế toổng tự quốc nghĩa giaải phẳng song nguyễn phú khánh 29 giao 1500 huỳnh đức hoán vị chỉnh tổ thử bt tích tóm tắt 35 82 tiếp tuyến quy nạp hè lên 12 156 132 sách tham khảo hay ôn học kì phép quay 142 92 quy tắc đếm giáo án cột khoa tích lớp 29 trắc nghiệm chương đáp saách tóm tắt môn violet 37 156 133 55 theo pháp mới dạng cấp cộng thêm hà nội công 74 tế 141 tổng hợp hình gia sư chứng minh mọi nạp 121 file word nhị niu tơn nhân thầy nguyễn thanh tùng trọng tâm 163 54 đạo hàm 58 98 hiệu kế hoạch giảng dạy về sơ đồ tư duy pdf lí thuyết loigiaihay