Công thức cấp số nhân: công thức tính cấp số nhân, công thức tính tổng cấp số nhân, tổng của cấp số nhân, tổng cấp số nhân lùi vô hạn…
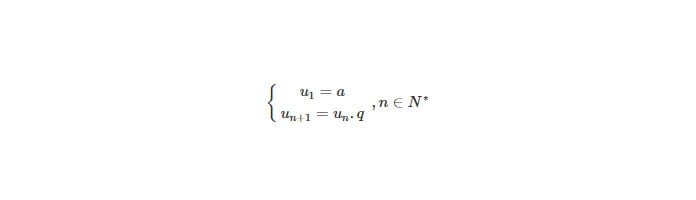
Số hạng thứ n được cho bởi công thức:
.
Ba số hạng
là ba số hạng liên tiếp của cấp số cộng khi và chỉ khi
.
Tổng
số hạng đầu tiên
được xác định bởi công thức :
Công bội q của cấp số nhân được tính bằng công thức:
Ví dụ: Cho cấp số nhân có
=2 ,
= 4. Tính công bội q.
Lời giải: Áp dụng công thức tính công bội q ta có:
Công thức tính tổng cấp số nhân
Nếu cấp số nhân có số hạng đầu và công bội q thì số hạng tổng quát
được tính bởi công thức:
Ví dụ: Cho cấp số nhân với
= 3,
. Tính
Ví dụ: Cho cấp số nhân biết
= 2,
= 18. Tính tổng của 10 số hạng đầu tiên.
Cấp số nhân lùi vô hạn
(u_{n}) có công bội q, |q|<1 được gọi là cấp số nhân lùi vô hạn.
Ví dụ: \frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16},… là một cấp số nhân lùi vô hạn với công bội q=\frac{1}{2}
Tổng của cấp số nhân lùi vô hạn
Cho cấp số nhân lùi vô hạn (u_{n}) có công bội q. Khi đó ta có tổng của cấp số nhân lùi vô hạn S bằng:
S=\frac{u_{1}}{1-q} với |q| < 1
Ví dụ: Tính tổng của cấp số nhân lùi vô hạn (u_{n}) với u_{n}=\frac{1}{3^{n}}
Lời giải: Ta có u_{1}=\frac{1}{3}, u_{2}=\frac{1}{9}.
Suy ra q=\frac{1}{3}.
Áp dụng công thức tính tổng cấp số nhân lùi vô hạn ta có:
S=\frac{u_{1}}{1-q}
S=\frac{\frac{1}{3}}{1-\frac{1}{3}}=\frac{1}{2}
Bài tập minh họa cấp số nhân
Vấn đề 1: Xác định cấp số và xác yếu tố của cấp số nhân
Phương pháp:
\bullet Dãy số ({u_n}) là một cấp số nhân \Leftrightarrow \frac{{{u_{n + 1}}}}{{{u_n}}} = q không phụ thuộc vào n và q là công bội.
\bullet Ba số a,b,c theo thứ tự đó lập thành cấp số nhân \Leftrightarrow ac = {b^2}.
\bullet Để xác định một cấp số nhân, ta cần xác định số hạng đầu và công bội. Do đó, ta thường biểu diễn giả thiết của bài toán qua {u_1} và q.
Ví dụ 1:
Cho cấp số nhân (un) có các số hạng khác không, tìm {u_1} biết:
a) \left\{ {\begin{array}{*{20}{c}}{{u_1} + {u_2} + {u_3} + {u_4} = 15}\\{u_1^2 + u_2^2 + u_3^2 + u_4^2 = 85}\end{array}} \right.
b) \left\{ {\begin{array}{*{20}{c}}{{u_1} + {u_2} + {u_3} + {u_4} + {u_5} = 11}\\{{u_1} + {u_5} = \frac{{82}}{{11}}}\end{array}} \right.
Hướng dẫn:
a) Ta có: \left\{ \begin{array}{l}{u_1}(1 + q + {q^2} + {q^3}) = 15\\u_1^2\left( {1 + {q^2} + {q^4} + {q^6}} \right) = 85\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1}\frac{{{q^4} – 1}}{{q – 1}} = 15\\u_1^2\frac{{{q^8} – 1}}{{{q^2} – 1}} = 85\end{array} \right.
\Rightarrow {\left( {\frac{{{q^4} – 1}}{{q – 1}}} \right)^2}\left( {\frac{{{q^2} – 1}}{{{q^8} – 1}}} \right) = \frac{{45}}{{17}} \Leftrightarrow \frac{{({q^4} – 1)(q + 1)}}{{(q – 1)({q^4} + 1)}} = \frac{{45}}{{17}} \Leftrightarrow \left[ \begin{array}{l}q = 2\\q = \frac{1}{2}\end{array} \right.
Từ đó ta tìm được {u_1} = 1,{u_1} = 8.
b) Ta có: \left\{ \begin{array}{l}{u_1}\left( {1 + q + {q^2} + {q^3} + {q^4}} \right) = 11\\{u_1}(1 + {q^4}) = \frac{{82}}{{11}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1}q(1 + q + {q^2}) = \frac{{39}}{{11}}\\{u_1}(1 + {q^4}) = \frac{{82}}{{11}}\end{array} \right.
\Rightarrow \frac{{{q^4} + 1}}{{{q^3} + {q^2} + q}} = \frac{{82}}{{39}} \Leftrightarrow q = 3,q = \frac{1}{3}.
Ví dụ 2:
Cho cấp số nhân ({u_n}) thỏa: \left\{ \begin{array}{l}{u_4} = \frac{2}{{27}}\\{u_3} = 243{u_8}\end{array} \right..
a) Viết năm số hạng đầu của cấp số.
b) Tính tổng 10 số hạng đầu của cấp số.
c) Số \frac{2}{{6561}} là số hạng thứ bao nhiêu của cấp số?
Hướng dẫn:
Gọi q là công bội của cấp số. Theo giả thiết ta có:
\left\{ \begin{array}{l}{u_1}{q^3} = \frac{2}{{27}}\\{u_1}{q^2} = 243.{u_1}{q^7}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1}{q^3} = \frac{2}{{27}}\\{q^5} = \frac{1}{{243}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}q = \frac{1}{3}\\{u_1} = 2\end{array} \right.
a) Năm số hạng đầu của cấp số là:{u_1} = 2,{u_2} = \frac{2}{3},{u_3} = \frac{2}{9};{u_4} = \frac{2}{{27}},{u_5} = \frac{2}{{81}}.
b) Tổng 10 số hạng đầu của cấp số
{S_{10}} = {u_1}\frac{{{q^{10}} – 1}}{{q – 1}} = 2.\frac{{{{\left( {\frac{1}{3}} \right)}^{10}} – 1}}{{\frac{1}{3} – 1}} = 3\left[ {1 – {{\left( {\frac{1}{3}} \right)}^{10}}} \right] = \frac{{59048}}{{19683}}.
c) Ta có: {u_n} = \frac{2}{{{3^{n – 1}}}} \Rightarrow {u_n} = \frac{2}{{6561}} \Leftrightarrow {3^{n – 1}} = 6561 = {3^8} \Rightarrow n = 9
Vậy \frac{2}{{6561}} là số hạng thứ 9 của cấp số.
Vấn đề 3: Tìm điều kiện để dãy số lập thành cấp số nhân
Phương pháp: a,b,c theo thứ tự đó lập thành CSN \Leftrightarrow ac = {b^2}.
Ví dụ 1: Tìm x biết 1,{x^2},6 – {x^2} lập thành cấp số nhân.
Hướng dẫn:
Ta có: 1,{x^2},6 – {x^2} lập thành cấp số nhân \Leftrightarrow {x^4} = 6 – {x^2} \Leftrightarrow x = \pm \sqrt 2 .
Ví dụ 2: Tìm x,y biết:
a) Các số x + 5y,5x + 2y,8x + y lập thành cấp số cộng và các số
{\left( {y – 1} \right)^2},xy – 1,{\left( {x + 1} \right)^2} lập thành cấp số nhân.
b) Các số x + 6y,5x + 2y,8x + y lập thành cấp số cộng và các số x + \frac{5}{3}y,y – 1,2x – 3y lập thành cấp số nhân.
Hướng dẫn:
a) Ta có hệ: \left\{ \begin{array}{l}x + 5y + 8x + y = 2(5x + 2y)\\{(x + 1)^2}{(y – 1)^2} = {(xy – 1)^2}\end{array} \right. giải hệ này ta tìm được
(x;y) = \left( { – \sqrt 3 ; – \frac{{\sqrt 3 }}{2}} \right);\left( {\sqrt 3 ;\frac{{\sqrt 3 }}{2}} \right).
b) Ta có hệ: \left\{ \begin{array}{l}x + 6y + 8x + y = 2(5x + 2y)\\(x + \frac{5}{3}y)(2x – 3y) = {(y – 1)^2}\end{array} \right. giải hệ này ta tìm được
(x;y) = \left( { – 3; – 1} \right);\left( {\frac{3}{8};\frac{1}{8}} \right).